

分析 (1)以D为原点,DA,DC,DD1所在直线分别为x轴,y轴,z轴,建立空间直角坐标系,利用向量法能证明DB⊥平面B1BCC1.
(2)求出平面A1BD的一个法向量和$\overrightarrow{B{C}_{1}}$,由此利用向量法能求出BC1与平面A1BD所成的角的正弦值.
(3)求出平面A1BD的一个法向量和平面C1BD的一个法向量,利用向量法能求出二面角A1-DB-C1的正弦值.
解答 证明:(1)以D为原点,DA,DC,DD1所在直线分别为x轴,y轴,z轴,
建立如图所示的空间直角坐标系,
则D(0,0,0),B(1,0,0),C1(0,2,2),A1(1,0,2),B1(1,1,2),C(0,2,0).(1分)
$\overrightarrow{DB}$=(1,1,0),$\overrightarrow{BC}$=(-1,1,0),$\overrightarrow{B{B}_{1}}$=(0,0,2),(2分)
$\overrightarrow{BD}•\overrightarrow{BC}$=-1+1=0,∴BD⊥BC,
$\overrightarrow{BD}•\overrightarrow{B{B}_{1}}$=0,∴BD⊥BB1,
又∵B1B∩BC=B,∴DB⊥平面B1BCC1.(4分
解:(2)设$\overrightarrow{n}$=(x,y,z)为平面A1BD的一个法向量.
由$\overrightarrow{n}⊥\overrightarrow{D{A}_{1}}$,$\overrightarrow{n}⊥\overrightarrow{DB}$,$\overrightarrow{D{A}_{1}}$=(1,0,2),$\overrightarrow{DB}$=(1,1,0),
得$\left\{\begin{array}{l}{x+2z=0}\\{x+y=0}\end{array}\right.$,取z=1,则$\overrightarrow{n}$=(-2,2,1).….(6分)
又$\overrightarrow{B{C}_{1}}$=(-1,1,2),设BC1与平面A1BD所成的角为θ,
则sinθ=|cos<$\overrightarrow{n}$,$\overrightarrow{B{C}_{1}}$>|=$\frac{|\overrightarrow{n}•\overrightarrow{B{C}_{1}}|}{|\overrightarrow{n}|•|\overrightarrow{B{C}_{1}}|}$=$\frac{6}{\sqrt{6}×9}$=$\frac{\sqrt{6}}{3}$,
即BC1与平面A1BD所成的角的正弦值$\frac{\sqrt{6}}{3}$.….(8分)
(3)由(2)知平面A1BD的一个法向量为$\overrightarrow{n}$=(-2,2,1)
设$\overrightarrow{m}$=(a,b,c)为平面C1BD的一个法向量,
由$\overrightarrow{m}⊥\overrightarrow{B{C}_{1}}$,$\overrightarrow{m}⊥\overrightarrow{DB}$,$\overrightarrow{B{C}_{1}}$=(-1,1,2),$\overrightarrow{DB}$=(1,1,0),
得$\left\{\begin{array}{l}{-a+b+2c=0}\\{a+b=0}\end{array}\right.$,取a=1,则$\overrightarrow{m}$=(1,-1,1).…(10分)
设$\overrightarrow{m}$与$\overrightarrow{n}$所成角为θ,则cosθ=$\frac{\overrightarrow{m}•\overrightarrow{n}}{|\overrightarrow{m}|•|\overrightarrow{n}|}$=$\frac{-3}{3×\sqrt{3}}$=-$\frac{1}{\sqrt{3}}$,
所以二面角A1-DB-C1的正弦值为$\frac{\sqrt{6}}{3}$.(13分)
点评 本题考查线面垂直的证明,考查线面角的正弦值的求法,考查二面角的正弦值的求法,是中档题,解题时要认真审题,注意向量法的合理运用.


科目:高中数学 来源:2016-2017学年内蒙古高二理上月考一数学理试卷(解析版) 题型:填空题
F1、F2是双曲线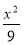 -
-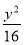 =1的两个焦点,P在双曲线上且满足|PF1|·|PF2|=
=1的两个焦点,P在双曲线上且满足|PF1|·|PF2|=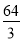 ,则∠F1PF2=__________.
,则∠F1PF2=__________.
查看答案和解析>>
科目:高中数学 来源:2016-2017学年江西吉安一中高二上段考一数学(理)试卷(解析版) 题型:解答题
如图1是图2的三视图,三棱锥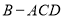 中,
中,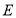 ,
,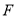 分别是棱
分别是棱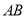 ,
,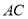 的中点.
的中点.
(1)求证: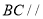 平面
平面 ;
;
(2)求三棱锥 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
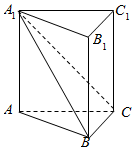 如图,在三棱柱ABC-A1B1C1中,AA1⊥平面ABC,平面A1BC⊥平面A1ABB1.
如图,在三棱柱ABC-A1B1C1中,AA1⊥平面ABC,平面A1BC⊥平面A1ABB1.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
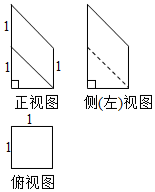 如图是某一几何体的三视图,则该几何体的体积是( )
如图是某一几何体的三视图,则该几何体的体积是( )| A. | $\frac{3}{4}$ | B. | 1 | C. | $\frac{5}{4}$ | D. | $\frac{3}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
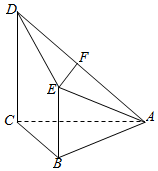 已知四棱锥A-BCDE,其中AC=BC=2,AC⊥BC,CD∥BE且CD=2BE,CD⊥平面ABC,F为AD的中点.
已知四棱锥A-BCDE,其中AC=BC=2,AC⊥BC,CD∥BE且CD=2BE,CD⊥平面ABC,F为AD的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,AD,CF是△ABC的两条高,AD,CF相交于点H,AD的延长线与△ABC的外接圆⊙O相交于点G,AE是⊙O的直径.
如图,AD,CF是△ABC的两条高,AD,CF相交于点H,AD的延长线与△ABC的外接圆⊙O相交于点G,AE是⊙O的直径.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com