
分析 (Ⅰ)设动圆圆心P,半径为r,利用两圆相切内切,两圆心距和两半径之间的关系列出PA和PB的关系式,正好符合椭圆的定义,利用定义法求轨迹方程即可.
(Ⅱ)假设存在这样的k,则直线方程可得与椭圆方程联立根据判别式求得k的范围,设出C,D点坐标,则根据韦达定理可表示出x1+x2和x1x2,当且仅当OC⊥OD时,以CD为直径的圆过原点O(0,0),求得y1y2+x1x2=0,根据直线方程和x1x2的表达式求得y1y2,建立等式求得k.
解答 解:(Ⅰ)设动圆圆心P(x,y),半径为r,⊙A的圆心为A(-$\sqrt{2}$,0),半径为2$\sqrt{3}$,
又因为动圆过点B,所以r=PB,
若动圆P与⊙A相内切,则有PA=2$\sqrt{3}$-r=2$\sqrt{3}$-PB,即PA+PB=2$\sqrt{3}$>AB=2$\sqrt{2}$
故P点的轨迹为以A和B为焦点的椭圆,且a=$\sqrt{3}$,c=$\sqrt{2}$,所以b2=a2-c2=1
所以动圆圆心的方程为$\frac{{x}^{2}}{3}+{y}^{2}$=1;
(Ⅱ)假设存在这样的k,
由直线y=kx+2与点P的轨迹方程联立,消去y,得(1+3k2)x2+12kx+9=0
则△=(12k)2-36(1+3k2)>0①
设C(x1,y1)、D(x2,y2),则x1+x2=-$\frac{12k}{1+3{k}^{2}}$,x1x2=$\frac{9}{1+3{k}^{2}}$
当且仅当OC⊥OD时,以CD为直径的圆过原点O(0,0),
即y1y2+x1x2=0
而y1•y2=(kx1+2)(kx2+2)=k2x1x2+2k(x1+x2)+4.
∴(k2+1)x1x2+2k(x1+x2)+4=0. ③
将②式代入③整理解得k=±$\frac{\sqrt{39}}{3}$
经验证,k=±$\frac{\sqrt{39}}{3}$,使①成立
综上可知,存在k=±$\frac{\sqrt{39}}{3}$,使得以CD为直径的圆过原点O(0,0).
点评 本题考查两圆的位置关系的应用和定义法求轨迹方程,考查直线与椭圆的位置关系,综合性较强.


科目:高中数学 来源: 题型:选择题
| A. | $[{3,\;\;\sqrt{10}}]$ | B. | [3,5] | C. | [3,4] | D. | $[{\sqrt{10},\;\;5}]$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
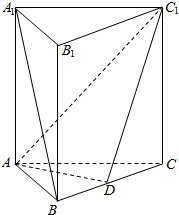 如图.在正三棱柱ABC-A1B1C1中,点D在棱BC上,AD⊥C1D.
如图.在正三棱柱ABC-A1B1C1中,点D在棱BC上,AD⊥C1D.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (2,3] | B. | [2,3] | C. | (2,3) | D. | (-∞,3] |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com