
【题目】若向量![]() 与向量
与向量![]() 的夹角为钝角,
的夹角为钝角, ![]() ,且当
,且当![]() 时,
时, ![]() (
(![]() )取最小值
)取最小值![]() ,向量
,向量![]() 满足
满足![]()
![]()
![]() ,则当
,则当![]()
![]() 取最大值时,
取最大值时, ![]() 等于( )
等于( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】A
【解析】设![]() =
=![]() ,
, ![]() =
=![]() ,
, ![]() =
=![]() ,如图:
,如图: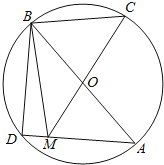
∵向量![]() ,
, ![]() 的夹角为钝角,
的夹角为钝角,
∴当与![]() 垂直时,
垂直时, ![]() 取最小值
取最小值![]() ,即
,即![]()
过点B作BD⊥AM交AM延长线于D,则BD=![]() ,
,
∵|![]() |=MB=2,∴MD=1,∠AMB=120°,即
|=MB=2,∴MD=1,∠AMB=120°,即![]() 与
与![]() 夹角为120°.
夹角为120°.
∵![]() ∴
∴![]() =0,
=0,
∴|![]() ||
||![]() |cos120°+
|cos120°+![]() |
|![]() |2=0,
|2=0,
∴|![]() |=2,即MA=2,
|=2,即MA=2,
∵![]()
![]()
![]() ,∴c的终点C在以AB为直径的圆O上,
,∴c的终点C在以AB为直径的圆O上,
∵O是AB中点,∴![]() =2
=2![]() ,
,
∴当M,O,C三点共线时, ![]() 取最大值,
取最大值,
∵AB=2![]() ,∴OB=0C=
,∴OB=0C=![]() ,
,
∵MA=MB=2,O是AB中点,∴MO⊥AB,
∴∠BOC=∠MOA=90°,
∴| ![]() |=BC=
|=BC=![]() OB=
OB=![]() .
.
故答案选:A.
点睛:这个题目考查了向量加法的三角形法则,向量垂直的坐标表示,向量模长的求法等知识方法,有一定的计算量.对于向量的小题常用的方法有:数形结合法,建系的方法,见模平方的意识,基底化的意识.


科目:高中数学 来源: 题型:
【题目】已知函数f(x)是定义在[-1,1]上的奇函数,在[0,1]上f(x)=2x+ln(x+1)-1.
(1)求函数f(x)的解析式;并判断f(x)在[-1,1]上的单调性(不要求证明);
(2)解不等式f(2x-1)+f(1-x2)≥0.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
, ![]() (
(![]() 为自然对数的底数).
为自然对数的底数).
(Ⅰ)当![]() 时,求函数
时,求函数![]() 在点
在点![]() 处的切线方程;
处的切线方程;
(Ⅱ)若函数![]() 有两个零点,试求
有两个零点,试求![]() 的取值范围;
的取值范围;
(Ⅲ)当![]() 时,
时, ![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某单位200名职工的年龄分布情况如图,现要从中抽取40名职工作样本.用系统抽样法,将全体职工随机按1~200编号,并按编号顺序平均分为40组(1~5号,6~10号,…,196~200号).若第5组抽出的号码为22,则第8组抽出的号码应是________.若用分层抽样法,则40岁的以下的年龄段应抽取__________人.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为 (
(![]() 为参数),将曲线
为参数),将曲线![]() 上各点的横坐标都缩短为原来的
上各点的横坐标都缩短为原来的![]() 倍,纵坐标坐标都伸长为原来的
倍,纵坐标坐标都伸长为原来的![]() 倍,得到曲线
倍,得到曲线![]() ,在极坐标系(与直角坐标系
,在极坐标系(与直角坐标系![]() 取相同的单位长度,且以原点
取相同的单位长度,且以原点![]() 为极点,以
为极点,以![]() 轴非负半轴为极轴)中,直线
轴非负半轴为极轴)中,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求直线![]() 和曲线
和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)设点![]() 是曲线
是曲线![]() 上的一个动点,求它到直线
上的一个动点,求它到直线![]() 的距离的最大值.
的距离的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商场为了了解顾客的购物信息,随机在商场收集了![]() 位顾客购物的相关数据如下表:
位顾客购物的相关数据如下表:
一次购物款(单位:元) |
|
|
|
|
|
顾客人数 |
|
|
|
|
|
统计结果显示![]() 位顾客中购物款不低于
位顾客中购物款不低于![]() 元的顾客占
元的顾客占![]() ,该商场每日大约有
,该商场每日大约有![]() 名顾客,为了增加商场销售额度,对一次购物不低于
名顾客,为了增加商场销售额度,对一次购物不低于![]() 元的顾客发放纪念品.
元的顾客发放纪念品.
(Ⅰ)试确定![]() ,
, ![]() 的值,并估计每日应准备纪念品的数量;
的值,并估计每日应准备纪念品的数量;
(Ⅱ)现有![]() 人前去该商场购物,求获得纪念品的数量
人前去该商场购物,求获得纪念品的数量![]() 的分布列与数学期望.
的分布列与数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com