
【题目】已知定义在R上的函数f(x)=2|x﹣m|﹣1(m为实数)为偶函数,记a=f(log0.53),b=f(log25),c=f(2m),则a,b,c的大小关系为 .
【答案】b>a>c
【解析】解:∵定义在R上的函数f(x)=2|x﹣m|﹣1(m为实数)为偶函数,
∴m=0,f(x)=2|x|﹣1,
∴x∈(﹣∞,0)时,f(x)是减函数,x∈(0,+∞)时,f(x)是增函数,
∵﹣1<log0.52<log0.53<log0.51=0,
log25>log24=2,
∴a=f(log0.53)= ![]() ﹣1∈(0,1),
﹣1∈(0,1),
b=f(log25)= ![]() ﹣1=4,
﹣1=4,
c=f(2m)=2|0|﹣1=0,
∴a,b,c的大小关系为b>a>c.
所以答案是:b>a>c.
【考点精析】关于本题考查的对数值大小的比较,需要了解几个重要的对数恒等式:![]() ,
,![]() ,
,![]() ;常用对数:
;常用对数:![]() ,即
,即![]() ;自然对数:
;自然对数:![]() ,即
,即![]() (其中
(其中![]() …)才能得出正确答案.
…)才能得出正确答案.


科目:高中数学 来源: 题型:
【题目】某城市理论预测2007年到2011年人口总数与年份的关系如表所示
年份2007+x(年) | 0 | 1 | 2 | 3 | 4 |
人口数y(十万) | 5 | 7 | 8 | 11 | 19 |
(1)请根据表提供的数据,求最小二乘法求出y关于x的线性回归方程;
(2)据此估计2012年该城市人口总数.
参考公式: 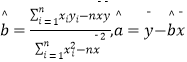 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从1到9这9个数字中任取3个偶数和3个奇数,组成无重复数字的六位数,
(1)有多少个偶数?
(2)若奇数排在一起且偶数排在一起,这样的六位数有多少个?
(3)若三个偶数不能相邻,这样的六位数有多少个?
(4)若三个偶数从左到右的排练顺序必须由大到小,这样的六位数有多少个?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知6只小白鼠有1只被病毒感染,需要通过对其化验病毒![]() 来确定是否感染.下面是两种化验方案:方案甲:逐个化验,直到能确定感染为止.方案乙:将6只分为两组,每组三个,并将它们混合在一起化验,若存在病毒
来确定是否感染.下面是两种化验方案:方案甲:逐个化验,直到能确定感染为止.方案乙:将6只分为两组,每组三个,并将它们混合在一起化验,若存在病毒![]() ,则表明感染在这三只当中,然后逐个化验,直到确定感染为止;若结果不含病毒
,则表明感染在这三只当中,然后逐个化验,直到确定感染为止;若结果不含病毒![]() ,则在另外一组中逐个进行化验.
,则在另外一组中逐个进行化验.
(1)求依据方案乙所需化验恰好为2次的概率.
(2)首次化验化验费为10元,第二次化验化验费为8元,第三次及其以后每次化验费都是6元,列出方案甲所需化验费用的分布列,并估计用方案甲平均需要体验费多少元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数 ![]() (x∈R).
(x∈R).
(1)求函数f(x)的值域;
(2)①判断函数f(x)的奇偶性;②用定义判断函数f(x)的单调性;
(3)解不等式f(1﹣m)+f(1﹣m2)<0.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解人们对于国家新颁布的“生育二胎放开”政策的热度,现在某市进行调查,随机抽调了50人,他们年龄的频数分布及支持“生育二胎”人数如下表:
年龄 | [5,15) | [15,25) | [25,35) | [35,45) | [45,55) | [55,65) |
频数 | 5 | 10 | 15 | 10 | 5 | 5 |
支持“生育二胎” | 4 | 5 | 12 | 8 | 2 | 1 |
(1)由以上统计数据填下面2×2列联表;
年龄不低于45岁的人 | 年龄低于45岁的人 | 合计 | |
支持“生育二胎” | a= | c= | |
不支持“生育二胎” | b= | d= | |
合计 |
(2)判断是否有99%的把握认为以45岁为分界点对“生育二胎放开”政策的支持度有差异.
P(K2≥k) | 0.050 | 0.010 | 0.001 |
k | 3.841 | 6.635 | 10.828 |
附表:K2= ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在多面体ABCDEF中,DE⊥平面ABCD,AD∥BC,平面BCEF∩平面ADEF=EF,∠BAD=60°,AB=AD=2,DE=1. 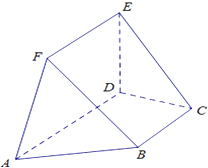
(1)求证:BC∥EF;
(2)求三棱锥B﹣ADE的体积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com