
【题目】心理健康教育老师对某班50个学生进行了心里健康测评,测评成绩满分为100分.成绩出来后,老师对每个成绩段的人数进行了统计,并得到如图4所示的频率分布直方图. 
(1)求a,并从频率分布直方图中求出成绩的众数和中位数;
(2)若老师从60分以下的人中选两个出来与之聊天,则这两人一个在(40,50]这一段,另一个在(50,60]这一段的概率是多少?
【答案】
(1)解:由(0.004+2a+0.02+0.024+0.036)×10=1,
解得a=0.008.
从频率分布直方图得知众数为75.
40至70的频率为0.32,40至80的频率为0.68,
故知中位数在70至80之间,设为x,
则(x﹣70)×0.036+0.32=0.5,
解得x=75,故中位数为75
(2)解:因为共有50个学生,
故从频率分布直方图中知(40,50]这一段有2人,(50,60]这一段有4人.
通过列表可知,从这6个人中选2个人共有n= ![]() =15种选法,
=15种选法,
从(40,50]和(50,60]这两段中各选一人共有m= ![]() =8种选法,
=8种选法,
故由古典概型知概率为p= ![]()
【解析】(1)由频率分布直方图中小矩形面积之和为1,能求出a的值.由频率分布直方图能求出众数、中位数.(2)因为共有50个学生,从频率分布直方图中知(40,50]这一段有2人,(50,60]这一段有4人.通过列表可知,从这6个人中选2个人共有n= ![]() =15种选法,从(40,50]和(50,60]这两段中各选一人共有m=
=15种选法,从(40,50]和(50,60]这两段中各选一人共有m= ![]() =8种选法,由古典概型能求出这两人一个在(40,50]这一段,另一个在(50,60]这一段的概率.
=8种选法,由古典概型能求出这两人一个在(40,50]这一段,另一个在(50,60]这一段的概率.
【考点精析】利用频率分布直方图对题目进行判断即可得到答案,需要熟知频率分布表和频率分布直方图,是对相同数据的两种不同表达方式.用紧凑的表格改变数据的排列方式和构成形式,可展示数据的分布情况.通过作图既可以从数据中提取信息,又可以利用图形传递信息.


 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案科目:高中数学 来源: 题型:
【题目】如图是某位篮球运动员8场比赛得分的茎叶图,其中一个数据染上污渍用x代替,则这位运动员这8场比赛的得分平均数不小于得分中位数的概率为( ) 
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知棱长为1的正方体ABCD﹣A1B1C1D1中,E,F分别是棱B1C1 , C1D1的中点. (Ⅰ)求AD1与EF所成角的大小;
(Ⅱ)求AF与平面BEB1所成角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直棱柱ABC﹣A1B1C1中,AC=BC=CC1= ![]() AB,E是线段CC1的中点,连接AE,B1E,AB1 , B1C,BC1 , 得到的图形如图所示. (Ⅰ)证明BC1⊥平面AB1C;
AB,E是线段CC1的中点,连接AE,B1E,AB1 , B1C,BC1 , 得到的图形如图所示. (Ⅰ)证明BC1⊥平面AB1C;
(Ⅱ)求二面角E﹣AB1﹣C的大小.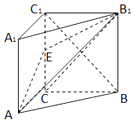
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若先将函数y= ![]() sin(x﹣
sin(x﹣ ![]() )+cos(x﹣
)+cos(x﹣ ![]() )图象上各点的纵坐标不变,横坐标缩短到原来的
)图象上各点的纵坐标不变,横坐标缩短到原来的 ![]() 倍,再将所得图象向左平移
倍,再将所得图象向左平移 ![]() 个单位,所得函数图象的一条对称轴的方程是( )
个单位,所得函数图象的一条对称轴的方程是( )
A.x= ![]()
B.x= ![]()
C.x= ![]()
D.x= ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=Asin(ωx+φ)(A>0,ω>0,﹣![]() <φ<
<φ<![]() , x∈R)的部分图象如图所示.
, x∈R)的部分图象如图所示.
(1)求函数y=f(x)的解析式;
(2)当x∈[﹣![]() ,
, ![]() ]时,求f(x)的取值范围.
]时,求f(x)的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com