
| ||
| 2 |
| ||
| 3 |
 解:设点A在平面α的射影是H,则AH为所求,作HE⊥OB,垂足为E,则OB⊥面AEH,
解:设点A在平面α的射影是H,则AH为所求,作HE⊥OB,垂足为E,则OB⊥面AEH,
| ||
| 2 |
| ||
| 3 |
| 2 |
| 3 |
| 1 |
| 3 |
| ||
| 3 |


 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源:2013-2014学年湖南汝城第一中学、长沙实验中学高三11月联考理数学卷(解析版) 题型:填空题
在平面几何里有射影定理:设△ABC的两边AB⊥AC,D是A点在BC上的射影,则AB2=BD·BC.拓展到空间,在四面体A—BCD中,DA⊥面ABC,点O是A在面BCD内的射影,且O在面BCD内,类比平面三角形射影定理,△ABC,△BOC,△BDC三者面积之间关系为 .
查看答案和解析>>
科目:高中数学 来源:2010-2011年福建省高二3月月考数学文卷 题型:填空题
在平面几何里有射影定理:“设△ABC的两边 ,D是A点在BC边上的射影,则
,D是A点在BC边上的射影,则 .”。拓展到空间,若三棱锥A-BCD的三个侧面ABC、ACD、ADB两两互相垂直,点O是顶点A在底面BCD上的射影且O点在△BCD内,类比平面上三角形的射影定理,△ABC、△BOC、△BCD三者的面积关系是
.”。拓展到空间,若三棱锥A-BCD的三个侧面ABC、ACD、ADB两两互相垂直,点O是顶点A在底面BCD上的射影且O点在△BCD内,类比平面上三角形的射影定理,△ABC、△BOC、△BCD三者的面积关系是
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
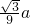

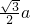
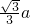
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com