Question

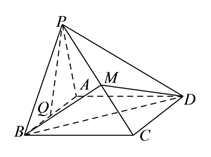
【题目】如图，在四棱锥P﹣ABCD中，PA⊥CD，AD∥BC，∠ADC=∠PAB=90°，BC=CD= AD．

（1）在平面PAD内找一点M，使得直线CM∥平面PAB，并说明理由；
（2）证明：平面PAB⊥平面PBD．

Answer 1

【答案】
（1）

证明： M为PD的中点，直线CM∥平面PAB．

取AD的中点E，连接CM，ME，CE，则ME∥PA，

∵ME平面PAB，PA平面PAB，

∴ME∥平面PAB．

∵AD∥BC，BC=AE，

∴ABCE是平行四边形，

∴CE∥AB．

∵CE平面PAB，AB平面PAB，

∴CE∥平面PAB．

∵ME∩CE=E，

∴平面CME∥平面PAB，

∵CM平面CME，

∴CM∥平面PAB；

（2）

解：∵PA⊥CD，∠PAB=90°，AB与CD相交，

∴PA⊥平面ABCD，

∵BD平面ABCD，

∴PA⊥BD，

由（1）及BC=CD= AD，可得∠BAD=∠BDA=45°，

∴∠ABD=90°，∴BD⊥AB，

∵PA∩AB=A，

∴BD⊥平面PAB，

∵BD平面PBD，

∴平面PAB⊥平面PBD

【解析】（1）M为PD的中点，直线CM∥平面PAB．取AD的中点E，连接CM，ME，CE，则ME∥PA，证明平面CME∥平面PAB，即可证明直线CM∥平面PAB；（II）证明：BD⊥平面PAB，即可证明平面PAB⊥平面PBD；本题主要考查了直线与平面平行的判定，平面与平面垂直的判定，考查空间想象能力、运算能力和推理论证能力，属于中档题．
【考点精析】本题主要考查了直线与平面平行的判定和平面与平面垂直的判定的相关知识点，需要掌握平面外一条直线与此平面内的一条直线平行，则该直线与此平面平行；简记为：线线平行，则线面平行；一个平面过另一个平面的垂线，则这两个平面垂直才能正确解答此题．