
(本题满分13分)设函数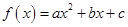 ,且
,且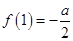 ,
,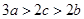 ,求证:(1)
,求证:(1)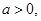 且
且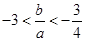 ;
;
(2)函数 在区间
在区间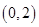 内至少有一个零点;
内至少有一个零点;
(3)设 是函数
是函数 的两个零点,则
的两个零点,则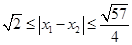 .
.
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
为了绿化城市,准备在如图所示的区域内修建一个矩形PQRC的草坪,且PQ//BC,RQ BC。另外
BC。另外 的内部有一文物保护区不能占用,经测量AB="100m," BC="80m," AE="30m," AF=20m,应如何设计才能使草坪的占地面积最大?
的内部有一文物保护区不能占用,经测量AB="100m," BC="80m," AE="30m," AF=20m,应如何设计才能使草坪的占地面积最大?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本题满分12分)已知某公司生产某品牌服装的年固定成本为10万元,每生产一千件,需要另投入2.7万元.设该公司年内共生产该品牌服装 千件并全部销售完,每千件的销售收入为
千件并全部销售完,每千件的销售收入为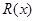 万元,且
万元,且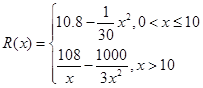 .
.
(I)写出年利润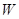 (万元)关于年产量
(万元)关于年产量 (千件)的函数关系式;
(千件)的函数关系式;
(Ⅱ)年生产量为多少千件时,该公司在这一品牌服装的生产中所获年利润最大?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
有一批运动服装原价为每套80元,两个商场均有销售,为了吸引顾客,两商场纷纷推出优惠政策。甲商场的优惠办法是:买一套减4元,买两套每套减8元,买三套每套减12元,......,依此类推,直到减到半价为止;乙商场的优惠办法是:一律7折。某单位欲为每位员工买一套运动服装,问选择哪个商场购买更省钱?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某汽车生产企业上年度生产一品牌汽车的投入成本为10万元/辆,出厂价为13万元/辆,年销售量为5000辆.本年度为适应市场需求,计划提高产品档次,适当增加投入成本,若每辆车投入成本增加的比例为 (0<
(0< <1
<1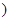 ,则出厂价相应提高的比例为0.7
,则出厂价相应提高的比例为0.7 ,年销售量也相应增加.已知年利润=(每辆车的出厂价-每辆车的投入成本)×年销售量.
,年销售量也相应增加.已知年利润=(每辆车的出厂价-每辆车的投入成本)×年销售量.
(1)若年销售量增加的比例为0.4 ,为使本年度的年利润比上年度有所增加,则投入成本增加的比例
,为使本年度的年利润比上年度有所增加,则投入成本增加的比例 应在什么范围内?
应在什么范围内?
(2)年销售量关于 的函数为
的函数为 ,则当
,则当 为何值时,本年度的年利润最大?最大利润为多少?
为何值时,本年度的年利润最大?最大利润为多少?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本题满分14分)建造一个容积为18立方米,深为2米的长方体有盖水池。如果池底和池壁每平方米的造价分别是200元和150元,那么如何建造,池的造价最低,为多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com