
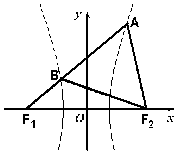
 如图,F1、F2分别是双曲线的左、右焦点,过F1的直线与双曲线的左、右两支分别相交于B、A两点,若△ABF2为等边三角形,则该双曲线的离心率为( )
如图,F1、F2分别是双曲线的左、右焦点,过F1的直线与双曲线的左、右两支分别相交于B、A两点,若△ABF2为等边三角形,则该双曲线的离心率为( )| A. | $\sqrt{3}$ | B. | $\sqrt{5}$ | C. | $\sqrt{7}$ | D. | 3 |
分析 根据双曲线的定义算出△AF1F2中,|AF1|=2a,|AF2|=4a,由△ABF2是等边三角形得∠F1AF2=120°,利用余弦定理算出c=$\sqrt{7}$a,结合双曲线离心率公式即可算出双曲线C的离心率.
解答 解:根据双曲线的定义,可得|BF1|-|BF2|=2a,
∵△ABF2是等边三角形,即|BF2|=|AB| ,
,
∴|BF1|-|BF2|=2a,即|BF1|-|AB|=|AF1|=2a
又∵|AF2|-|AF1|=2a,
∴|AF2|=|AF1|+2a=4a,
∵△AF1F2中,|AF1|=2a,|AF2|=4a,∠F1AF2=120°,
∴|F1F2|2=|AF1|2+|AF2|2-2|AF1|•|AF2|cos120°,
即4c2=4a2+16a2-2×2a×4a×(-$\frac{1}{2}$)=28a2,解之得c=$\sqrt{7}$a,
由此可得双曲线C的离心率e=$\frac{c}{a}$=$\sqrt{7}$.
故选:C.
点评 本题考查双曲线的简单性质的应用,题目考查经过双曲线左焦点的直线被双曲线截得弦AB与右焦点构成等边三角形,求双曲线的离心率,着重考查了双曲线的定义和简单几何性质等知识,属于中档题.


 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案 高效智能课时作业系列答案
高效智能课时作业系列答案科目:高中数学 来源: 题型:选择题
| A. | 30° | B. | 60° | C. | 120° | D. | 150° |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-$\frac{5}{4}$,1) | B. | ($\frac{3}{4}$,1) | C. | ($\frac{4}{5}$,1) | D. | (-1,$\frac{3}{4}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{5}}{5}$ | B. | $\frac{2\sqrt{5}}{5}$ | C. | 1 | D. | $\frac{\sqrt{17}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com