
【题目】在一个![]() 的方格表的每个方格内填入1或
的方格表的每个方格内填入1或![]() ,如果任意一格内的数都等于与它有公共边的那些方格内所填数的乘积,则称这种填法是“成功”的.求“成功”填法的总数.
,如果任意一格内的数都等于与它有公共边的那些方格内所填数的乘积,则称这种填法是“成功”的.求“成功”填法的总数.
【答案】1
【解析】
假设存在某种成功填法,其中含有![]() .
.
首先证明:若此种成功填法关于中间一列(行)对称,则中间一列(行)全为1.
设![]() ,
,![]() .若
.若![]() ,由
,由![]() ,得
,得![]() .
.
同理,![]() ,…,
,…,![]() .
.
若![]() ,同理可得
,同理可得![]() .
.
因此,若![]() ,则
,则![]() .这样,
.这样,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,…,
,…,![]() ,
,![]() ,
,![]() .从而
.从而![]() ,矛盾.
,矛盾.
因此,中间一列(行)全为1.
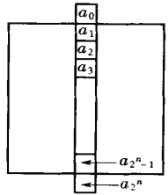
其次,若此种成功填法不关于中间一列对称,先将此种填法沿中间一列翻转![]() ,得另一种填法,再将两种填法处于相同位置的数相乘,就得到关于中间一列对称的成功填法,其中含有
,得另一种填法,再将两种填法处于相同位置的数相乘,就得到关于中间一列对称的成功填法,其中含有![]() .此种成功填法可进一步转化为既关于中间一行,又关于中间一列对称的成功填法,其中含有
.此种成功填法可进一步转化为既关于中间一行,又关于中间一列对称的成功填法,其中含有![]() .
.
对这样的![]() 的成功填法,去掉中间一行与中间一列的所有1,就可得到4个
的成功填法,去掉中间一行与中间一列的所有1,就可得到4个![]() 的成功填法,至少有一个其中含有
的成功填法,至少有一个其中含有![]() .对这个成功填法,一直重复上面的操作,最终可得到一个
.对这个成功填法,一直重复上面的操作,最终可得到一个![]() 的成功填法,其中含有
的成功填法,其中含有![]() ,但中间一行和中间一列全为1,这与成功填法的定义矛盾.
,但中间一行和中间一列全为1,这与成功填法的定义矛盾.
因此,对任意成功填法,其中一定不含有![]() .故成功填法只有1种,即每个方格中均填1.
.故成功填法只有1种,即每个方格中均填1.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知下列命题:
①在线性回归模型中,相关指数![]() 越接近于1,表示回归效果越好;
越接近于1,表示回归效果越好;
②两个变量相关性越强,则相关系数r就越接近于1;
③在回归直线方程![]() 中,当解释变量
中,当解释变量![]() 每增加一个单位时,预报变量
每增加一个单位时,预报变量![]() 平均减少0.5个单位;
平均减少0.5个单位;
④两个模型中残差平方和越小的模型拟合的效果越好.
⑤回归直线![]() 恒过样本点的中心
恒过样本点的中心![]() ,且至少过一个样本点;
,且至少过一个样本点;
⑥若![]() 的观测值满足
的观测值满足![]() ≥6.635,我们有99%的把握认为吸烟与患肺病有关系,那么在100个吸烟的人中必有99人患有肺病;
≥6.635,我们有99%的把握认为吸烟与患肺病有关系,那么在100个吸烟的人中必有99人患有肺病;
⑦从统计量中得知有95%的把握认为吸烟与患肺病有关系,是指有5%的可能性使得推断出现错误. 其中正确命题的序号是__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某年级100名学生期中考试数学成绩(单位:分)的频率分布直方图如图所示,其中成绩分组区间是[50,60),[60,70),[70,80),[80,90),[90,100].
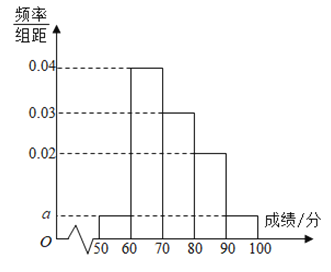
(1)求图中a的值,并根据频率分布直方图估计这100名学生数学成绩的平均分;
(2)从[70,80)和[80,90)分数段内采用分层抽样的方法抽取5名学生,求在这两个分数段各抽取的人数;
(3)现从第(2)问中抽取的5名同学中任选2名参加某项公益活动,求选出的两名同学均来自[70,80)分数段内的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学拟在高一下学期开设游泳选修课,为了了解高一学生喜欢游泳是否与性别有关,现从高一学生中抽取![]() 人做调查,得到
人做调查,得到![]() 列联表:
列联表:
喜欢游泳 | 不喜欢游泳 | 合计 | |
男生 | 40 | ||
女生 | 30 | ||
合计 | 100 |
且已知在![]() 个人中随机抽取
个人中随机抽取![]() 人,抽到喜欢游泳的学生的概率为
人,抽到喜欢游泳的学生的概率为![]() .
.
(1)请完成上面的列联表;
(2)根据列联表的数据,是否有![]() 的把握认为喜欢游泳与性别有关?并说明你的理由.
的把握认为喜欢游泳与性别有关?并说明你的理由.
附: (其中
(其中![]() )和临界值表:
)和临界值表:
| 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 0.45 | 0.708 | 1.32 | 2.072 | 2.706 | 3.84 | 5.024 | 6.635 | 7.879 | 10.83 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某旅游爱好者计划从3个亚洲国家A1,A2,A3和3个欧洲国家B1,B2,B3中选择2个国家去旅游.
(1)若从这6个国家中任选2个,求这2个国家都是亚洲国家的概率;
(2)若从亚洲国家和欧洲国家中各选1个,求这两个国家包括A1,但不包括B1的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某机构为了解某地区中学生在校月消费情况,随机抽取了 100名中学生进行调查.如图是根据调査的结果绘制的学生在校月消费金额的频率分布直方图.已知![]() 三个金额段的学生人数成等差数列,将月消费金额不低于550元的学生称为“高消费群”.
三个金额段的学生人数成等差数列,将月消费金额不低于550元的学生称为“高消费群”.
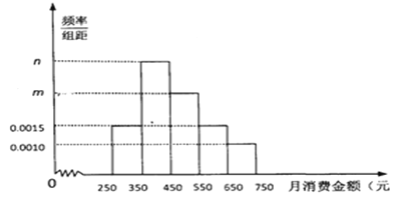
(1)求![]() 的值,并求这100名学生月消费金额的样本平均数
的值,并求这100名学生月消费金额的样本平均数![]() (同一组中的数据用该组区间的中点值作代表);
(同一组中的数据用该组区间的中点值作代表);
(2)根据已知条件完成下面![]() 列联表,并判断能否有
列联表,并判断能否有![]() 的把握认为“高消费群”与性别有关?
的把握认为“高消费群”与性别有关?

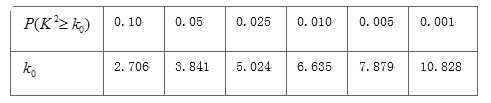
附: ![]() (其中
(其中![]() 样本容量)
样本容量)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com