
【题目】如图,在平面直角坐标系xOy中,已知以M为圆心的圆M:x2+y2-12x-14y+60=0及其上一点A(2,4).
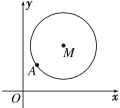
(1)设圆N与x轴相切,与圆M外切,且圆心N在直线x=6上,求圆N的标准方程;
(2)设平行于OA的直线l与圆M相交于B,C两点,且BC=OA,
求直线l的方程.
 作业辅导系列答案
作业辅导系列答案科目:高中数学 来源: 题型:
【题目】如图,直线![]() 与圆
与圆 ![]() 且与椭圆
且与椭圆![]() 相交于
相交于![]() 两点.
两点.

(1)若直线![]() 恰好经过椭圆的左顶点,求弦长
恰好经过椭圆的左顶点,求弦长![]()
(2)设直线![]() 的斜率分别为
的斜率分别为![]() ,判断
,判断![]() 是否为定值,并说明理由
是否为定值,并说明理由
(3)求![]() ,面积的最小值.
,面积的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
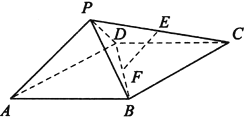
【题目】如图,四棱锥P—ABCD中,ABCD为矩形,△PAD为等腰直角三角形,
∠APD=90°,面PAD⊥面ABCD,且AB=1,AD=2,E、F分别为PC和BD的中点.
(1)证明:EF∥面PAD;
(2)证明:面PDC⊥面PAD;
(3)求四棱锥P—ABCD的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】直角坐标系![]() 和极坐标系
和极坐标系![]() 的原点与极点重合,
的原点与极点重合, ![]() 轴正半轴与极轴重合,单位长度相同,在直角坐标系下,曲线C的参数方程为
轴正半轴与极轴重合,单位长度相同,在直角坐标系下,曲线C的参数方程为![]() 为参数)。
为参数)。
(1)在极坐标系下,曲线C与射线![]() 和射线
和射线![]() 分别交于A,B两点,求
分别交于A,B两点,求![]() 的面积;
的面积;
(2)在直角坐标系下,直线![]() 的参数方程为
的参数方程为 (
(![]() 为参数),求曲线C与直线
为参数),求曲线C与直线![]() 的交点坐标。
的交点坐标。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商场经销一批进价为每件30元的商品,在市场试销中发现,此商品的销售单价x(元)与日销售量y(件)之间有如下表所示的关系:
x | 30 | 40 | 45 | 50 |
y | 60 | 30 | 15 | 0 |
在所给的坐标图纸中,根据表中提供的数据,描出实数对(x,y)的对应点,并确定y与x的一个函数关系式;

(2)设经营此商品的日销售利润为P元,根据上述关系,写出P关于x的函数关系式,并指出销售单价x为多少元时,才能获得最大日销售利润?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着节假日外出旅游人数增多,倡导文明旅游的同时,生活垃圾处理也面临新的挑战,某海滨城市沿海有![]() 三个旅游景点,在岸边
三个旅游景点,在岸边![]() 两地的中点处设有一个垃圾回收站点
两地的中点处设有一个垃圾回收站点![]() (如图),
(如图),![]() 两地相距10
两地相距10![]() ,从回收站
,从回收站![]() 观望
观望![]() 地和
地和![]() 地所成的视角为
地所成的视角为![]() ,且
,且![]() ,设
,设![]() ;
;
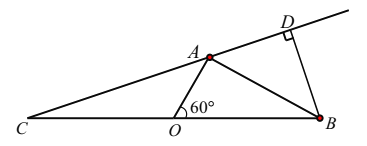
(1)用![]() 分别表示
分别表示![]() 和
和![]() ,并求出
,并求出![]() 的取值范围;
的取值范围;
(2)某一时刻太阳与![]() 三点在同一直线,此时
三点在同一直线,此时![]() 地到直线
地到直线![]() 的距离为
的距离为![]() ,求
,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系中,以原点O为极点,x轴的正半轴为极轴建立极坐标系,点A的极坐标为(3, ![]() ),点B的极坐标为(6,
),点B的极坐标为(6, ![]() ),曲线C:(x﹣1)2+y2=1
),曲线C:(x﹣1)2+y2=1
(1)求曲线C和直线AB的极坐标方程;
(2)过点O的射线l交曲线C于M点,交直线AB于N点,若|OM||ON|=2,求射线l所在直线的直角坐标方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() 是空间两条直线,
是空间两条直线, ![]() 是空间两个平面,则下列命题中不正确的是( )
是空间两个平面,则下列命题中不正确的是( )
A. 当![]() 时,“
时,“![]() ”是“
”是“![]() ”的充要条件
”的充要条件
B. 当![]() 时,“
时,“![]() ”是“
”是“![]() ”的充分不必要条件
”的充分不必要条件
C. 当![]() 时,“
时,“![]() ”是“
”是“![]() ”的必要不充分条件
”的必要不充分条件
D. 当![]() 时,“
时,“![]() ”是“
”是“![]() ”的充分不必要条件
”的充分不必要条件
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com