练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    19．已知抛物线y2=4x截直线y=x+b所得弦长为4，求b的值．

    分析 将直线的方程代入抛物线的方程，消去y得到关于x的一元二次方程，再结合根系数的关系利用弦长公式即可求得b值，从而解决问题．

    解答 解：设A（x1，y1）、B（x1，y2）．
    联立抛物线y2=4x，直线y=x+b，消去y得方程：x2+（2b-4）x+b2=0
    x1+x2=4-2b．x1x2=b2，
    |AB|=$\sqrt{2}$•$\sqrt{（4-2b）^{2}-4{b}^{2}}$=4
    解得b=$\frac{1}{2}$．

    点评 本题主要考查了直线与抛物线相交求解弦长，关键是根据方程的根与系数的关系表示AB，这是圆锥曲线的考查的热点之一．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

    9．已知Rt△ABC的斜边AB的长为4，设|$\overrightarrow{PC}$|=1，则$\overrightarrow{PA}$•$\overrightarrow{PB}$的取值范围是[-3，5]．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    10．已知△ABC中，a=4，b=5，A=30°．下列对三角形解的情况的判断中，正确的是（　　）
    A．一解B．两解C．无解D．一解或无解

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    7．编写一个程序，求使不等式1+$\frac{1}{2}$+$\frac{1}{3}$+…+$\frac{1}{n}$＞10成立的最小自然数n的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    14．函数y=log${\;}_{\frac{1}{2}}$sin（2πx+$\frac{π}{4}$）的单调递减区间是（k-$\frac{1}{8}$，k+$\frac{1}{8}$]，k∈Z．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    4．如图，在平行六面体ABCD-A1B1C1D1中，M为AC与D的交点，若$\overrightarrow{{A}_{1}{B}_{1}}$=$\overrightarrow{a}$，$\overrightarrow{A{{\;}_{1}D}_{1}}$=$\overrightarrow{b}$，$\overrightarrow{{A}_{1}A}$=$\overrightarrow{c}$，用基底{$\overrightarrow{a}$，$\overrightarrow{b}$，$\overrightarrow{c}$}表示向量$\overrightarrow{{C}_{1}M}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    11．log${\;}_{\sqrt{2}}$27×log${\;}_{\frac{1}{3}}$8=（　　）
    A．12B．18C．-18D．-$\frac{9}{2}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    8．若f（x）=$\frac{x-1}{x+1}$，则dy|x=1=$\frac{1}{2}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

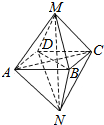    11．如图所示的几何体，关于其结构特征，下列说法不正确的是（　　）
    A．该几何体是由两个同底的四棱锥组成的几何体
    B．该几何体有12条棱、6个顶点
    C．该几何体有8个面，并且各面均为三角形
    D．该几何体有9个面，其中一个面是四边形，其余均为三角形

    查看答案和解析>>

    同步练习册答案