
【题目】已知函数f(x)=asinx![]() cos2x+1(a,b∈R).
cos2x+1(a,b∈R).
(1)当a=1,且![]()
![]() 时,求f(x)的值域;
时,求f(x)的值域;
(2)若存在实数![]()
![]() 使得
使得![]() 成立,求实数a的取值范围.
成立,求实数a的取值范围.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】分析:(1)根据三角函数的诱导公式得到f(x)=2![]() +sinx,再由二次函数解析式,讨论轴和区间的关系得到最值;(2)存在实数x使得函数|f(x)|≥a2成立,∴存在t∈[﹣1,1]使得函数|2t2+at|≥a2成立,即存在t∈[﹣1,1]使得2t2+at﹣a2≥0或2t2+at+a2≤0成立.
+sinx,再由二次函数解析式,讨论轴和区间的关系得到最值;(2)存在实数x使得函数|f(x)|≥a2成立,∴存在t∈[﹣1,1]使得函数|2t2+at|≥a2成立,即存在t∈[﹣1,1]使得2t2+at﹣a2≥0或2t2+at+a2≤0成立.
详解:
(1)当a=1时,f(x)=sinx﹣cos2x+1=sinx﹣(1﹣2sin2x)+1=2sin2x+sinx
=2![]() ﹣
﹣![]() ;
;
![]() 时,sinx∈[﹣1,1],
时,sinx∈[﹣1,1],
∴sinx=﹣![]() 时,f(x)取得最小值﹣
时,f(x)取得最小值﹣![]() ,sinx=1时,f(x)取得最大值3,
,sinx=1时,f(x)取得最大值3,
∴f(x)的值域为[﹣![]() ,3];
,3];
(2)f(x)=asinx﹣cos2x+1=asinx+2sin2x=2sin2x+asinx,
设t=sinx,则t∈[﹣1,1],代入原函数得y=2t2+at,
∵存在实数x使得函数|f(x)|≥a2成立,
∴存在t∈[﹣1,1]使得函数|2t2+at|≥a2成立,
∴存在t∈[﹣1,1]使得2t2+at﹣a2≥0或2t2+at+a2≤0成立,
①当a=0时,2t2≥0或2t2≤0成立,
②当a≠0时,由于2t2+at+a2≤0的△=﹣7a2<0,不等式无解,
由2t2+at﹣a2≥0得(2t﹣a)(t+a)≥0,
当a>0时,2t2+at﹣a2≥0的解集是(﹣∞,﹣a]∪[![]() ,+∞),
,+∞),
由题意可得,![]() ≤1或﹣a≥﹣1,解得0<a≤2,
≤1或﹣a≥﹣1,解得0<a≤2,
当a<0时,2t2+at﹣a2≥0的解集是(﹣∞,![]() ]∪[﹣a,+∞),
]∪[﹣a,+∞),
由题意可得,﹣a≤1或![]() ≥﹣1,解得﹣2≤a<0,
≥﹣1,解得﹣2≤a<0,
综上,实数a的取值范围是[﹣2,2].


 作业辅导系列答案
作业辅导系列答案 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,曲线 ![]() ,曲线C2的参数方程为:
,曲线C2的参数方程为: ![]() ,(θ为参数),以O为极点,x轴的正半轴为极轴的极坐标系.
,(θ为参数),以O为极点,x轴的正半轴为极轴的极坐标系.
(1)求C1 , C2的极坐标方程;
(2)射线 ![]() 与C1的异于原点的交点为A,与C2的交点为B,求|AB|.
与C1的异于原点的交点为A,与C2的交点为B,求|AB|.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线l1的方程为3x+4y﹣12=0.
(1)若直线l2与l1平行,且过点(﹣1,3),求直线l2的方程;
(2)若直线l2与l1垂直,且l2与两坐标轴围成的三角形面积为4,求直线l2的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线l1的方程为3x+4y﹣12=0.
(1)若直线l2与l1平行,且过点(﹣1,3),求直线l2的方程;
(2)若直线l2与l1垂直,且l2与两坐标轴围成的三角形面积为4,求直线l2的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点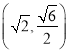 与点
与点![]() 都在椭圆
都在椭圆![]() 上.
上.
(1)求椭圆![]() 的方程;
的方程;
(2)若![]() 的左焦点、左顶点分别为
的左焦点、左顶点分别为![]() ,则是否存在过点
,则是否存在过点![]() 且不与
且不与![]() 轴重合的直线
轴重合的直线![]() (记直线
(记直线![]() 与椭圆
与椭圆![]() 的交点为
的交点为![]() ),使得点
),使得点![]() 在以线段
在以线段![]() 为直径的圆上;若存在,求出直线
为直径的圆上;若存在,求出直线![]() 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
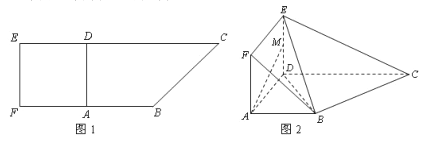
【题目】如图 1,在直角梯形![]() 中,
中, ![]() ,且
,且![]() .现以
.现以![]() 为一边向形外作正方形
为一边向形外作正方形![]() ,然后沿边
,然后沿边![]() 将正方形
将正方形![]() 翻折,使
翻折,使![]() 平面与平面
平面与平面![]() 垂直,
垂直, ![]() 为
为![]() 的中点,如图 2.
的中点,如图 2.
(1)求证: ![]() 平面
平面![]() ;
;
(2)求证: ![]() 平面
平面![]() ;
;
(3)求点![]() 到平面
到平面![]() 的距离.
的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】直线l:ax+ ![]() y﹣1=0与x,y轴的交点分别为A,B,直线l与圆O:x2+y2=1的交点为C,D.给出下列命题:p:a>0,S△AOB=
y﹣1=0与x,y轴的交点分别为A,B,直线l与圆O:x2+y2=1的交点为C,D.给出下列命题:p:a>0,S△AOB= ![]() ,q:a>0,|AB|<|CD|.则下面命题正确的是( )
,q:a>0,|AB|<|CD|.则下面命题正确的是( )
A.p∧q
B.¬p∧¬q
C.p∧¬q
D.¬p∧q
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com