
 在△ABC中,AB=AC,D为BC边上一点,E为AD上一点,且满足∠BDE=2∠CED=∠BAC.求证:BD=2CD.
在△ABC中,AB=AC,D为BC边上一点,E为AD上一点,且满足∠BDE=2∠CED=∠BAC.求证:BD=2CD. 分析 作DO∥AB交AC于O,取F为△EDC的外接圆与AC的交点,利用△ADO∽△ABE,即得$\frac{OD}{AE}=\frac{AD}{AB}=\frac{AD}{AC}=\frac{AF}{AE}$,即可得出结论.
解答 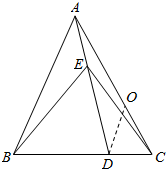 证明:作DO∥AB交AC于O.
证明:作DO∥AB交AC于O.
则由AB=AC易知OD=OC,且∠DOC=∠A=2∠CED,
所以O为△EDC的外心,
取F为△EDC的外接圆与AC的交点,则OF=OC=OD,∠ACE=∠ADF.
所以△ACE∽△ADF,即有AD/AC=AF/AE.
再由DO∥AB,∠ADO=∠BAE,∠AOD=180-∠DOC=180°-∠A=180°-∠BED=∠AEB,
所以△ADO∽△ABE,即得$\frac{OD}{AE}=\frac{AD}{AB}=\frac{AD}{AC}=\frac{AF}{AE}$.
故AF=OD=OC=CF,从而AO=2OC.
由DO∥AB得:BD=2CD.
点评 本题考查三角形相似的证明,考查比例的性质,考查学生分析解决问题的能力,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | (x-4)2+(y-6)2=5 | B. | (x-4)2+(y-6)2=10 | C. | (x-2)2+(y-1)2=5 | D. | (x-6)2+(y-4)2=25 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com