
【题目】为了解某班学生喜爱打篮球是否与性别有关,对该班40名学生进行了问卷调查,得到了如下的![]() 列联表:
列联表:
男生 | 女生 | 总计 | |
喜爱打篮球 | 19 | 15 | 34 |
不喜爱打篮球 | 1 | 5 | 6 |
总计 | 20 | 20 | 40 |
(1)在女生不喜爱打篮球的5个个体中,随机抽取2人,求女生甲被选中的概率;
(2)判断能否在犯错误的概率不超过![]() 的条件下认为喜爱篮球与性别有关?
的条件下认为喜爱篮球与性别有关?
附: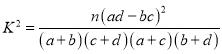 ,其中
,其中![]() .
.
| 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | <>0.005 | 0.001 |
| 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案科目:高中数学 来源: 题型:
【题目】某电视台举行一个比赛类型的娱乐节目, ![]() 两队各有六名选手参赛,将他们首轮的比赛成绩作为样本数据,绘制成茎叶图如图所示,为了增加节目的趣味性,主持人故意将
两队各有六名选手参赛,将他们首轮的比赛成绩作为样本数据,绘制成茎叶图如图所示,为了增加节目的趣味性,主持人故意将![]() 队第六位选手的成绩没有给出,并且告知大家
队第六位选手的成绩没有给出,并且告知大家![]() 队的平均分比
队的平均分比![]() 队的平均分多4分,同时规定如果某位选手的成绩不少于21分,则获得“晋级”.
队的平均分多4分,同时规定如果某位选手的成绩不少于21分,则获得“晋级”.
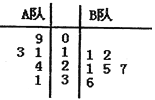
(1)根据茎叶图中的数据,求出![]() 队第六位选手的成绩;
队第六位选手的成绩;
(2)主持人从![]() 队所有选手成绩中随机抽2个,求至少有一个为“晋级”的概率;
队所有选手成绩中随机抽2个,求至少有一个为“晋级”的概率;
(3)主持人从![]() 两队所有选手成绩分别随机抽取2个,记抽取到“晋级”选手的总人数为
两队所有选手成绩分别随机抽取2个,记抽取到“晋级”选手的总人数为![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以
为参数),以![]() 为极点,以
为极点,以![]() 轴的正半轴为极轴,建立极坐标系,直线
轴的正半轴为极轴,建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为 ![]()
(1)求曲线![]() 的普通方程和直线
的普通方程和直线![]() 的直角坐标方程;
的直角坐标方程;
(2)设点![]() ,若直线
,若直线![]() 与曲线
与曲线![]() 相交于
相交于![]() ,
,![]() 两点,且
两点,且![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知一动圆P与定圆![]() 外切,且与直线
外切,且与直线![]() 相切,记动点P的轨迹为曲线E.
相切,记动点P的轨迹为曲线E.
(1)求曲线E的方程;
(2)过点![]() 作直线l与曲线E交于不同的两点B、C,设BC中点为Q,问:曲线E上是否存在一点A,使得
作直线l与曲线E交于不同的两点B、C,设BC中点为Q,问:曲线E上是否存在一点A,使得![]() 恒成立?如果存在,求出点A的坐标;如果不存在,说明理由.
恒成立?如果存在,求出点A的坐标;如果不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】新闻出版业不断推进供给侧结构性改革,深入推动优化升级和融合发展,持续提高优质出口产品供给,实现了行业的良性发展.下面是2012年至2016年我国新闻出版业和数字出版业营收增长情况,则下列说法错误的是( )
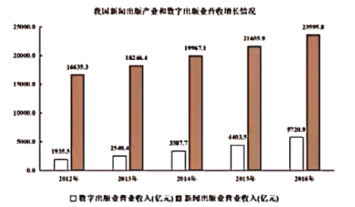
A. 2012年至2016年我国新闻出版业和数字出版业营收均逐年增加
B. 2016年我国数字出版业营收超过2012年我国数字出版业营收的2倍
C. 2016年我国新闻出版业营收超过2012年我国新闻出版业营收的1.5倍
D. 2016年我国数字出版营收占新闻出版营收的比例未超过三分之一
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设椭圆![]()
![]() 的离心率为
的离心率为![]() ,圆
,圆![]() 与
与![]() 轴正半轴交于点
轴正半轴交于点![]() ,圆
,圆![]() 在点
在点![]() 处的切线被椭圆
处的切线被椭圆![]() 截得的弦长为
截得的弦长为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)设圆![]() 上任意一点
上任意一点![]() 处的切线交椭圆
处的切线交椭圆![]() 于点
于点![]() ,
,![]() ,试判断
,试判断![]() 是否为定值?若为定值,求出该定值;若不是定值,请说明理由.
是否为定值?若为定值,求出该定值;若不是定值,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() (
(![]() ,且
,且![]() 、
、![]() ).设关于
).设关于![]() 的不等式
的不等式![]() 的解集为
的解集为![]() ,且方程
,且方程![]() 的两实根为
的两实根为![]() 、
、![]() .
.
(1)若![]() ,完成下列问题:
,完成下列问题:
①求![]() 、
、![]() 的关系式;
的关系式;
②若![]() 、
、![]() 都是负整数,求
都是负整数,求![]() 的解析式;
的解析式;
(2)若![]() ,求证:
,求证: ![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com