
【题目】已知函数f(x)=﹣x2+ax+1﹣lnx.
(1)当a=3时,求函数f(x)的单调递增区间;
(2)若f(x)在区间(0, ![]() )上是减函数,求实数a的取值范围.
)上是减函数,求实数a的取值范围.
【答案】
(1)解:当a=3时,f(x)=﹣x2+3x+1﹣lnx
∴ ![]()
解f′(x)>0,
即:2x2﹣3x+1<0
函数f(x)的单调递增区间是 ![]() .
.
(2)解:f′(x)=﹣2x+a﹣ ![]() ,
,
∵f(x)在 ![]() 上为减函数,
上为减函数,
∴x∈ ![]() 时﹣2x+a﹣
时﹣2x+a﹣ ![]() ≤0恒成立.
≤0恒成立.
即a≤2x+ ![]() 恒成立.
恒成立.
设 ![]() ,则
,则 ![]()
∵x∈ ![]() 时,
时, ![]() >4,
>4,
∴g′(x)<0,
∴g(x)在 ![]() 上递减,
上递减,
∴g(x)>g( ![]() )=3,
)=3,
∴a≤3
【解析】(1)求单调区间,先求导,令导函数大于等于0即可.(2)已知f(x)在区间(0, ![]() )上是减函数,即f′(x)≤0在区间(0,
)上是减函数,即f′(x)≤0在区间(0, ![]() )上恒成立,然后用分离参数求最值即可.
)上恒成立,然后用分离参数求最值即可.
【考点精析】通过灵活运用函数的单调性和函数单调性的性质,掌握注意:函数的单调性是函数的局部性质;函数的单调性还有单调不增,和单调不减两种;函数的单调区间只能是其定义域的子区间 ,不能把单调性相同的区间和在一起写成其并集即可以解答此题.


科目:高中数学 来源: 题型:
【题目】【选修4-5:不等式选讲】
已知函数f(x)=|x+1|+|x-3|.
(1)若关于x的不等式f(x)<a有解,求实数a的取值范围:
(2)若关于x的不等式f(x)<a的解集为(b, ![]() ),求a+b的值.
),求a+b的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设全集为实数集R,函数f(x)=lg(2x﹣1)的定义域为A,集合B={x||x|﹣a≤0}(a∈R)
(1)若a=2,求A∪B和A∩B
(2)若RA∪B=RA,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱锥P-ABC中,PA⊥AB,PA⊥BC,AB⊥BC,PA=AB=BC=2,D为线段AC的中点,E为线段PC上一点.

(1)求证:PA⊥BD;
(2)求证:平面BDE⊥平面PAC;
(3)当PA∥平面BDE时,求三棱锥E-BCD的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=a( ![]() )x+bx2+cx(α∈R,b≠0,c∈R),若{x|f(x)=0}={x|f(f(x))=0}≠,则实数c的取值范围为( )
)x+bx2+cx(α∈R,b≠0,c∈R),若{x|f(x)=0}={x|f(f(x))=0}≠,则实数c的取值范围为( )
A.(0,4)
B.[0,4]
C.(0,4]
D.[0,4)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在△OAB中,点P为线段AB上的一个动点(不包含端点),且满足 ![]() =λ
=λ ![]() .
. 
(1)若λ= ![]() ,用向量
,用向量 ![]() ,
, ![]() 表示
表示 ![]() ;
;
(2)若| ![]() |=4,|
|=4,| ![]() |=3,且∠AOB=60°,求
|=3,且∠AOB=60°,求 ![]()
![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了得到函数y=2sin( ![]() +
+ ![]() ),x∈R的图象,只需要把函数y=2sinx,x∈R的图象上所有的点( )
),x∈R的图象,只需要把函数y=2sinx,x∈R的图象上所有的点( )
A.向左平移 ![]() 个单位,再把所得各点的横坐标缩短为原来的
个单位,再把所得各点的横坐标缩短为原来的 ![]() 倍(纵坐标不变)
倍(纵坐标不变)
B.向右平移 ![]() 个单位,再把所得各点的横坐标缩短为原来的
个单位,再把所得各点的横坐标缩短为原来的 ![]() 倍(纵坐标不变)
倍(纵坐标不变)
C.向左平移 ![]() 个单位,再把所得各点的横坐标缩短为原来的3倍(纵坐标不变)
个单位,再把所得各点的横坐标缩短为原来的3倍(纵坐标不变)
D.向右平移 ![]() 个单位,再把所得各点的横坐标缩短为原来的3倍(纵坐标不变)
个单位,再把所得各点的横坐标缩短为原来的3倍(纵坐标不变)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法正确的是( ) 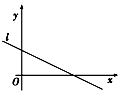
A.已知购买一张彩票中奖的概率为 ![]() ,则购买1000张这种彩票一定能中奖
,则购买1000张这种彩票一定能中奖
B.互斥事件一定是对立事件
C.如图,直线l是变量x和y的线性回归方程,则变量x和y相关系数在﹣1到0之间
D.若样本x1 , x2 , …xn的方差是4,则x1﹣1,x2﹣1,…xn﹣1的方差是3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,现要在边长为100m的正方形ABCD内建一个交通“环岛”.以正方形的四个顶点为圆心在四个角分别建半径为xm(x不小于9)的扇形花坛,以正方形的中心为圆心建一个半径为 ![]() m的圆形草地.为了保证道路畅通,岛口宽不小于60m,绕岛行驶的路宽均小于10m.
m的圆形草地.为了保证道路畅通,岛口宽不小于60m,绕岛行驶的路宽均小于10m. 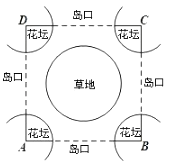
(1)求x的取值范围;(运算中 ![]() 取1.4)
取1.4)
(2)若中间草地的造价为a元/m2 , 四个花坛的造价为 ![]() 元/m2 , 其余区域的造价为
元/m2 , 其余区域的造价为 ![]() 元/m2 , 当x取何值时,可使“环岛”的整体造价最低?
元/m2 , 当x取何值时,可使“环岛”的整体造价最低?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com