函数f(x)的定义域D={x|x≠0},且满足对于任意x1,x2∈D,有f(x1•x2)=f(x1)+f(x2).
(1)求f(1)与f(-1)的值;
(2)判断函数的奇偶性并证明;
(3)若x>1时,f(x)>0,求证f(x)在区间(0,+∞)上是增函数;
(4)在(3)的条件下,若f(4)=1,求不等式f(3x+1)≤2的解集.
解:(1)令x
1=x
2=1,有f(1×1)=f(1)+f(1),解得f(1)=0.
令x
1=x
2=-1,有f[(-1)×(-1)]=f(-1)+f(-1)=f(1)=0,解得f(-1)=0.
(2)令x
1=-1,x
2=x,有f(-x)=f(-1)+f(x)=f(x),定义域关于原点对称可得f(x)是偶函数.
(3)设x
1,x
2∈(0,+∞)且x
1<x
2,则

,
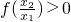
,
则
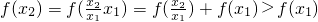
,
∴f(x)在区间(0,+∞)上是增函数.
(4)f(16)=f(4×4)=f(4)+f(4)=2,
由f(3x+1)≤2变形为f(3x+1)≤f(16).
∵f(x)为偶函数,∴f(-x)=f(x)=f(|x|),在(3)的条件下有f[|3x+1|]≤f(16)
∴|3x+1|≤16且3x+1≠0,解得x∈
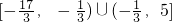
.
分析:(1)利用该抽象函数满足的函数值关系的性质,赋两个自变量相应的值,可以求解出f(1)与f(-1)的值;
(2)根据函数的奇偶性的定义结合已知条件得出f(-x)与f(x)的关系是解决本题的关键,注意对自变量赋合适的函数值;
(3)根据单调性的定义,任取定义区间的两个自变量,比较其函数值得出f(x)在区间(0,+∞)上的递增性质;
(4)利用(3)中函数的单调性,将函数值的关系转化为相应自变量的关系列出关于x的不等式是解决本题的关键.
点评:本题考查抽象函数问题的解决方法,考查赋值法求给定自变量处函数值,赋值法确定函数奇偶性、单调性的方法,充分发挥定义的引领作用.考查函数单调性在转化求解自变量时的应用作用.

 ,
,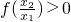 ,
,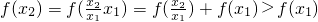 ,
,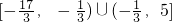 .
.

 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案