
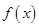 满足
满足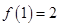 ,且当
,且当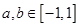 ,
,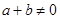 时,有
时,有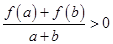 .
.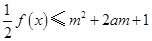 对所有
对所有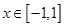 ,
,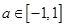 恒成立,
恒成立,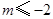 或
或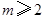 或
或 .
.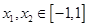 ,且
,且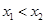 , 则
, 则
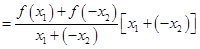 4分
4分 ,
,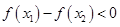
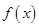 是[-1,1]上的增函数 6分
是[-1,1]上的增函数 6分
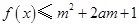 对所有
对所有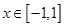 ,
,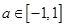 恒成立,
恒成立,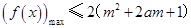 , 11分
, 11分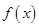 是[-1,1]上的增函数 ∴
是[-1,1]上的增函数 ∴
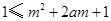 对任意的
对任意的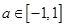 恒成立 3分
恒成立 3分 ,则只须
,则只须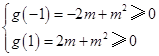 ,
,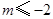 或
或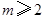 或
或 15分
15分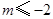 或
或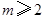 或
或 . 16分
. 16分

科目:高中数学 来源:不详 题型:解答题
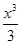 -x2-2ax(a∈R).
-x2-2ax(a∈R).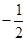 时,方程f(1-x)=
时,方程f(1-x)=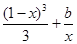 有实根,求实数b的最大值.
有实根,求实数b的最大值.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
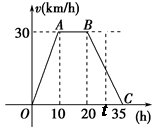
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
 对应密文:
对应密文: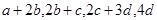 ,当接收方收到密文14,9,23,28时,解密得到的明文为( )
,当接收方收到密文14,9,23,28时,解密得到的明文为( )A.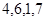 | B.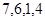 | C.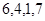 | D.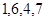 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
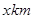 ,建在C处的垃圾处理厂对城A和城B的总影响度为
,建在C处的垃圾处理厂对城A和城B的总影响度为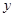 ,统计调查表明:垃圾处理厂对城A的影响度与所选地点到城A的距离的平方成反比,比例系数为4;对城B的影响度与所选地点到城B的距离的平方成反比,比例系数为k,当垃圾处理厂建在AB的中点时,对A和城B的总影响度为0.065。
,统计调查表明:垃圾处理厂对城A的影响度与所选地点到城A的距离的平方成反比,比例系数为4;对城B的影响度与所选地点到城B的距离的平方成反比,比例系数为k,当垃圾处理厂建在AB的中点时,对A和城B的总影响度为0.065。

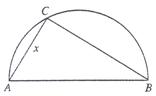
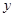 表示成
表示成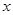 的函数;
的函数; (2)判断弧AB上是否存在一点,使建在此处的垃圾处理厂对城A和城B的总影响度最小?若存在,求出该点到城A的距离;若不存在,说明理由。
(2)判断弧AB上是否存在一点,使建在此处的垃圾处理厂对城A和城B的总影响度最小?若存在,求出该点到城A的距离;若不存在,说明理由。查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com