
某中学为丰富教工生活,国庆节举办教工趣味投篮比赛,有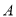 、
、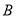 两个定点投篮位置,在
两个定点投篮位置,在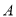 点投中一球得2分,在
点投中一球得2分,在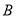 点投中一球得3分.其规则是:按先
点投中一球得3分.其规则是:按先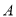 后
后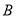 再
再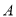 的顺序投
的顺序投
篮.教师甲在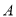 和
和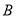 点投中的概率分别是
点投中的概率分别是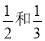 ,且在
,且在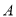 、
、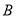 两点投中与否相互独立.
两点投中与否相互独立.
(1)若教师甲投篮三次,试求他投篮得分X的分布列和数学期望;
(2)若教师乙与甲在A、B点投中的概率相同,两人按规则各投三次,求甲胜乙的概率.
(1)分布列详见解析,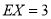 ;(2)
;(2)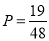 .
.
【解析】
试题分析:本题主要考查独立事件、随机事件的分布列和数学期望等基础知识,考查学生的分析问题解决问题的能力和计算能力.第一问,先分析出教师甲投篮得分的不同情况,利用独立事件的概率的计算公式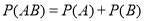 计算每一种情况的概率,列出分布列,利用
计算每一种情况的概率,列出分布列,利用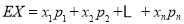 求出数学期望;第二问,先分析出甲胜乙的情况,包括甲得2分,3分,4分,5分,7分的情况,利用第一问的分布列的表格,第一种情况:甲得2分,乙得0分;第二种情况:甲得3分,乙得0分或2分;第三种情况::甲得4分,乙得0分或2分或3分;第四种情况:甲得5分,乙得0分或2分或3分或4分;第五种情况:甲得7分,乙得0分或2分或3分或4分或5分,求出每一种情况的概率再相见得到所求结论.
求出数学期望;第二问,先分析出甲胜乙的情况,包括甲得2分,3分,4分,5分,7分的情况,利用第一问的分布列的表格,第一种情况:甲得2分,乙得0分;第二种情况:甲得3分,乙得0分或2分;第三种情况::甲得4分,乙得0分或2分或3分;第四种情况:甲得5分,乙得0分或2分或3分或4分;第五种情况:甲得7分,乙得0分或2分或3分或4分或5分,求出每一种情况的概率再相见得到所求结论.
试题解析:设“教师甲在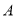 点投中”的事件为
点投中”的事件为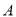 ,“教师甲在
,“教师甲在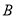 点投中”的事件为
点投中”的事件为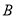 .
.
(1)根据题意知X的可能取值为0,2,3,4,5,7
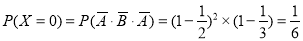 ,
,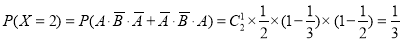
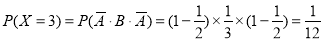
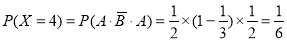
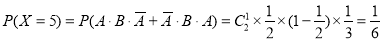
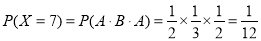 6分
6分
X | 0 | 2 | 3 | 4 | 5 | 7 |
P |
|
|
|
|
|
|
所以X的分布列是:
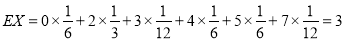 8分
8分
(2)教师甲胜乙包括:甲得2分、3分、4分、5分、7分五种情形.
这五种情形之间彼此互斥,因此,所求事件的概率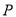 为:
为:
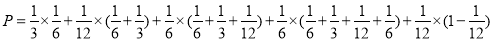
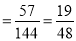 12分
12分
考点:独立事件、随机事件的分布列和数学期望.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:2013-2014学年安徽省皖北协作区高三年级联考理科数学试卷(解析版) 题型:选择题
设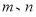 是不同的直线,
是不同的直线,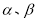 是不同的平面,有以下四个命题:
是不同的平面,有以下四个命题:
①若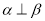 ,
,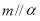 ,则
,则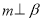
②若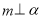 ,
,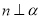 ,则
,则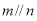
③若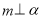 ,
,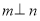 ,则
,则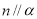
④若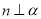 ,
,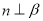 ,则
,则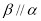 .
.
其中真命题的序号为( )
A. ①③ B. ②③ C. ①④ D. ②④
查看答案和解析>>
科目:高中数学 来源:2013-2014学年安徽省皖北协作区高三年级联考文科数学试卷(解析版) 题型:选择题
若 ,且
,且
 则“
则“ ”是“
”是“ ”的( )
”的( )
A、充分不必要条件
B、必要不充分条件
C、充要条件
D、既不充分也不必要
查看答案和解析>>
科目:高中数学 来源:2013-2014学年安徽省安庆市高三第二次模拟考试理科数学试卷(解析版) 题型:选择题
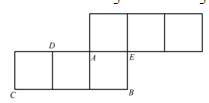
右图是棱长为2的正方体的表面展开图,则多面体 的体积为( )
的体积为( )
A. 2 B.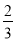 C.
C.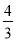 D.
D.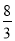
查看答案和解析>>
科目:高中数学 来源:2013-2014学年安徽省“皖西七校”高三年级联合考试理科数学试卷(解析版) 题型:解答题
学校操场边有一条小沟,沟沿是两条长150米的平行线段,沟宽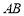 为2米,,与沟沿垂直的平面与沟的交线是一段抛物线,抛物线的顶点为
为2米,,与沟沿垂直的平面与沟的交线是一段抛物线,抛物线的顶点为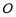 ,对称轴与地面垂直,沟深2米,沟中水深1米.
,对称轴与地面垂直,沟深2米,沟中水深1米.
(1)求水面宽;
(2)如图1所示形状的几何体称为柱体,已知柱体的体积为底面积乘以高,求沟中的水有多少立方米?


(3)现在学校要把这条水沟改挖(不准填土)成截面为等腰梯形的沟,使沟的底面与地面平行,沟深不变,两腰分别与抛物线相切(如图2),问改挖后的沟底宽为多少米时,所挖的土最少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com