
分析 利用同角三角函数的基本关系求得tanα的值,从而得到要求式子的值.
解答 解:(1)∵2sinα+cosα=0,∴tanα=-$\frac{1}{2}$,∴$\frac{2cosα-sinα}{sinα+cosα}$=$\frac{2-tanα}{tanα+1}$=$\frac{2-(-\frac{1}{2})}{-\frac{1}{2}+1}$=5.
(2)$\frac{sinα}{si{n}^{3}α-co{s}^{3}α}$=$\frac{sinα}{(sinα-cosα)•{(sin}^{2}α+sinαcosα{+cos}^{2}α)}$=$\frac{sinα}{(sinα-cosα)•(1+sinαcosα)}$
=$\frac{tanα}{(tanα-1)•(1+\frac{sinαcosα}{{sin}^{2}α{+cos}^{2}α})}$=$\frac{tanα}{(tanα-1)•(1+\frac{tanα}{{tan}^{2}α+1})}$=$\frac{-\frac{1}{2}}{(-\frac{1}{2}-1)•(1+\frac{-\frac{1}{2}}{\frac{1}{4}+1})}$=$\frac{5}{3}$.
点评 本题主要考查同角三角函数的基本关系、立方差公式的应用,属于基础题.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{4}$ | B. | $\frac{4}{3}$ | C. | $\frac{3}{4}$或 $\frac{4}{3}$ | D. | -$\frac{3}{4}$或-$\frac{4}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 小指 | B. | 中指 | C. | 食指 | D. | 大拇指 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
| 广告费用 x(万元) | 4 | 2 | 3 | 5 |
| 销售额y(万元) | 49 | 26 | 39 | 54 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\frac{1}{2}$ | B. | $\frac{1}{2}$ | C. | $-\frac{{\sqrt{3}}}{2}$ | D. | $\frac{{\sqrt{3}}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
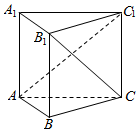 三棱柱ABC-A1B1C1中,△ABC是等边三角形,AA1⊥底面ABC,AB=2,AA1=$\sqrt{2}$,则异面直线AC1与B1C所成的角的大小是( )
三棱柱ABC-A1B1C1中,△ABC是等边三角形,AA1⊥底面ABC,AB=2,AA1=$\sqrt{2}$,则异面直线AC1与B1C所成的角的大小是( )| A. | 30° | B. | 60° | C. | 90° | D. | 120° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com