
【题目】在三棱锥P—ABC中,PB![]() 平面ABC,AB
平面ABC,AB![]() BC,AB=PB=2,BC=2
BC,AB=PB=2,BC=2![]() ,E、G分别为PC、PA的中点.
,E、G分别为PC、PA的中点.
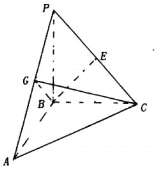
(1)求证:平面BCG![]() 平面PAC;
平面PAC;
(2)假设在线段AC上存在一点N,使PN![]() BE,求
BE,求![]() 的值;
的值;
(3)在(2)的条件下,求直线![]() 与平面
与平面![]() 所成角的正弦值
所成角的正弦值
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】近些年学区房的出现折射出现行教育体制方面的弊端造成了教育资源的分配不均衡.为此某市出台了政策:自2019年1月1日起,在该市新登记并取得房屋不动产权证书的住房用于申请入学的将不再对应一所学校,实施多校划片.有关部门调查了该市某名校对应学区内建筑面积不同的户型,得到了以下数据:
![]()
(1)试建立房屋价格y关于房屋建筑面积的x的线性回归方程;
(2)若某人计划消费不超过100万元购置学区房,根据你得到的回归方程估计此人选房时建筑面积最大为多少?(保留到小数点后一位数字)
参考公式: ,
,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校实行选科走班制度,张毅同学的选择是物理生物政治这三科,且物理在 A 层班级,生物在 B 层班级,该校周一上午课程安排如下表所示,张毅选择三个科目的课各上一节, 另外一节上自习,则他不同的选课方法有( )
第一节 | 第二节 | 第三节 | 第四节 |
地理 B 层 2 班 | 化学 A 层 3 班 | 地理 A 层 1 班 | 化学 A 层 4 班 |
生物 A 层 1 班 | 化学 B 层 2 班 | 生物 B 层 2 班 | 历史 B 层 1 班 |
物理 A 层 1 班 | 生物 A 层 3 班 | 物理 A 层 2 班 | 生物 A 层 4 班 |
物理 B 层 2 班 | 生物 B 层 1 班 | 物理 B 层 1 班 | 物理 A 层 4 班 |
政治 1 班 | 物理 A 层 3 班 | 政治 2 班 | 政治 3 班 |
A.8 种B.10 种C.12 种D.14 种
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的长轴为
的长轴为![]() ,
,![]() 分别为椭圆C的左、右顶点,P是椭圆C上异于
分别为椭圆C的左、右顶点,P是椭圆C上异于![]() 的动点,且
的动点,且![]() 面积的最大值为
面积的最大值为![]() .
.
(1)求椭圆C的方程;
(2)过点![]() 的直线l交椭圆C于
的直线l交椭圆C于![]() 两点,D为椭圆上一点,O为坐标原点,且满足
两点,D为椭圆上一点,O为坐标原点,且满足![]() ,其中
,其中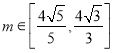 ,求直线l的斜率k的取值范围.
,求直线l的斜率k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ax+bx(a>0,b>0,a≠1,b≠1).设a=2,b=![]() .
.
(1)求方程f(x)=2的根;
(2)若对于任意x∈R,不等式f(2x)≥mf(x)-6恒成立,求实数m的最大值;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着经济的发展,轿车已成为人们上班代步的一种重要工具.现将某人三年以来每周开车从家到公司的时间之和统计如图所示.
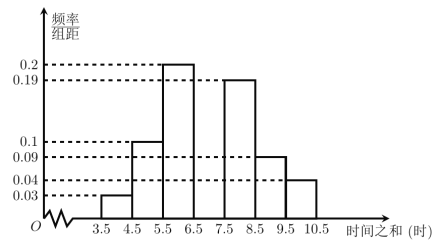
(1)求此人这三年以来每周开车从家到公司的时间之和在![]() (时)内的频率;
(时)内的频率;
(2)求此人这三年以来每周开车从家到公司的时间之和的平均数(每组取该组的中间值作代表);
(3)以频率估计概率,记此人在接下来的四周内每周开车从家到公司的时间之和在![]() (时)内的周数为
(时)内的周数为![]() ,求
,求![]() 的分布列以及数学期望.
的分布列以及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】福彩是利国利民游戏,其刮刮乐之《蓝色奇迹》:如图(1)示例,刮开票面看到最左侧一列四个两位数字为“我的号码”,最上行四个两位数为“中奖号码”,这八个两位数是00至99这一百个数字随机产生的,若两个数字相同即中得其相交线上的奖金,奖金可以累加.小明买的一张《蓝色奇迹》刮刮乐如图(2),除了一个“我的号码”外,他已经刮开票面上其它所有数字,依据目前的信息,小明从这张刮刮乐得到的奖金额高于600元的概率为(无所得税)( )


图(1) 图(2)
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com