
【题目】随着生活节奏的加快以及智能手机的普及,外卖点餐逐渐成为越来越多用户的餐饮消费习惯,由此催生了一批外卖点餐平台。已知某外卖平台的送餐费用与送餐距离有关(该平台只给5千米范围内配送),为调査送餐员的送餐收入,现从该平台随机抽取80名点外卖的用户进行统计,按送餐距离分类统计结果如下表:

以这80名用户送餐距离位于各区间的频率代替送餐距离位于该区间的概率。
(1)若某送餐员一天送餐的总距离为120千米,试估计该送餐员一天的送餐份数;(四舍五入精确到整数)
(2)若该外卖平台给送餐员的送餐费用与送餐距离有关,规定2千米内为短距离,每份3元,2千米到4千米为中距离,每份5元,超过4千米为远距离,每份10元。
(i)记X为送餐员送一份外卖的收入(单位:元),求X的分布列和数学期望;
(ii)若送餐员一天的目标收入不低于180元,试估计一天至少要送多少份外卖?
 一本好题口算题卡系列答案
一本好题口算题卡系列答案科目:高中数学 来源: 题型:
【题目】学校艺术节对同一类的![]() ,
,![]() ,
,![]() ,
,![]() 四项参赛作品,只评一项一等奖,在评奖揭晓前,甲、乙、丙、丁四位同学对这四项参赛作品预测如下:
四项参赛作品,只评一项一等奖,在评奖揭晓前,甲、乙、丙、丁四位同学对这四项参赛作品预测如下:
甲说:“是![]() 或
或![]() 作品获得一等奖”;
作品获得一等奖”;
乙说:“![]() 作品获得一等奖”;
作品获得一等奖”;
丙说:“![]() ,
,![]() 两项作品未获得一等奖”;
两项作品未获得一等奖”;
丁说:“是![]() 作品获得一等奖”.
作品获得一等奖”.
若这四位同学中只有两位说的话是对的,则获得一等奖的作品是__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“既要金山银山,又要绿水青山”。某风景区在一个直径![]() 为
为![]() 米的半圆形花圆中设计一条观光线路。打算在半圆弧上任选一点
米的半圆形花圆中设计一条观光线路。打算在半圆弧上任选一点![]() (与
(与![]() 不重合),沿
不重合),沿![]() 修一条直线段小路,在路的两侧(注意是两侧)种植绿化带;再沿弧
修一条直线段小路,在路的两侧(注意是两侧)种植绿化带;再沿弧![]() 修一条弧形小路,在小路的一侧(注意是一侧)种植绿化带,小路与绿化带的宽度忽略不计。
修一条弧形小路,在小路的一侧(注意是一侧)种植绿化带,小路与绿化带的宽度忽略不计。

(1)设![]() (弧度),将绿化带的总长度表示为
(弧度),将绿化带的总长度表示为![]() 的函数
的函数![]() ;
;
(2)求绿化带的总长度![]() 的最大值。
的最大值。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P-ABCD中,AB//CD,且![]() .
.

(1)证明:平面PAB⊥平面PAD;
(2)若PA=PD=AB=DC, ![]() ,求二面角A-PB-C的余弦值.
,求二面角A-PB-C的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对定义在[0,1]上,并且同时满足以下两个条件的函数f(x)称为G函数.
①对任意的x∈[0,1],总有f(x)≥0;
②当x1≥0,x2≥0,x1+x2≤1时,总有f(x1+x2)≥f(x1)+f(x2)成立.已知函数g(x)=x2与h(x)=2x﹣b是定义在[0,1]上的函数.
(1)试问函数g(x)是否为G函数?并说明理由;
(2)若函数h(x)是G函数,求实数b组成的集合.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为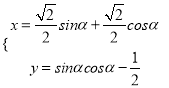 (
(![]() 为参数),若以直角坐标系中的原点为极点,
为参数),若以直角坐标系中的原点为极点, ![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() (
(![]() 为实数.)
为实数.)
(1)求曲线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)若曲线![]() 与曲线
与曲线![]() 有公共点,求
有公共点,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com