(I)解:求导函数可得:f′(x)=lnx+2(x>0)
令f′(x)>0可得x>e
-2;令f′(x)<0可得0<x<e
-2,
∴函数在(0,e
-2)上单调减,在(e
-2,+∞)上单调增
∴x=e
-2时,函数f(x)取到最小值,最小值为-e
-2;
(II)解:设F(x)=ax
2+f′(x)=ax
2+lnx+2,则F′(x)=2ax+

=
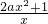
(x>0)
当a≥0时,∵x>0,∴F′(x)>0恒成立,∴函数F(x)单调增区间为(0,+∞);
当a<0时,∵x>0,令F′(x)>0,可得
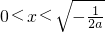
;令F′(x)>0,可得
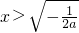
∴函数F(x)单调增区间为
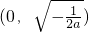
,单调减区间为
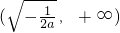
;
(III)证明:y=f′(x)的定义域为(0,+∞)
∵f″(x)=

>0,∴y=f′(x)在(0,+∞)上为增函数
∴0<f′(x
2)<k<f′(x
1)
∴
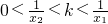
∴
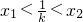
.
分析:(I)求导函数,确定函数的单调性,从而可得函数f(x)的最小值;
(II)确定函数的定义域,求导函数,对a讨论,利用导数的正负,考查函数的单调区间;
(III)确定y=f′(x)的定义域,求导函数,确定y=f′(x)在(0,+∞)上为增函数,从而可得结论.
点评:本题考查导数知识的运用,考查函数的单调性,考查函数的最值,考查导数的几何意义,属于中档题.

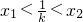 .
. =
=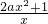 (x>0)
(x>0)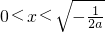 ;令F′(x)>0,可得
;令F′(x)>0,可得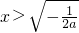
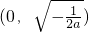 ,单调减区间为
,单调减区间为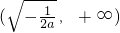 ;
; >0,∴y=f′(x)在(0,+∞)上为增函数
>0,∴y=f′(x)在(0,+∞)上为增函数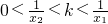
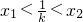 .
.

 53随堂测系列答案
53随堂测系列答案 已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<