
【题目】一袋中装有6个黑球,4个白球.如果不放回地依次取出2个球.求:
(1)第1次取到黑球的概率;
(2)第1次和第2次都取到黑球的概率;
(3)在第1次取到黑球的条件下,第2次又取到黑球的概率.
科目:高中数学 来源: 题型:
【题目】设有两个命题:p:关于x的不等式x2+2x-4-a≥0对一切x∈R恒成立;q:已知a≠0,a≠±1,函数y=-|a|x在R上是减函数,若p∧q为假命题,p∨q为真命题,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某车间为了规定工时定额,需要确定加工零件所花费的时间,为此做了四次试验,得到的数据如下:
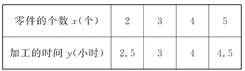
(1)在给定的坐标系中画出表中数据的散点图;
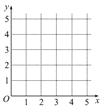
(2)求出y关于x的线性回归方程![]() ,并在坐标系中画出回归直线;
,并在坐标系中画出回归直线;
(3)试预测加工10个零件需要多少小时?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】当今,手机已经成为人们不可或缺的交流工具,人们常常把喜欢玩手机的人冠上了名号“低头族”,手机已经严重影响了人们的生活,一媒体为调查市民对低头族的认识,从某社区的500名市民中,随机抽取![]() 名市民,按年龄情况进行统计的频率分布表和频率分布直方图如图:
名市民,按年龄情况进行统计的频率分布表和频率分布直方图如图:

(1)求出表中的![]() 的值,并补全频率分布直方图;
的值,并补全频率分布直方图;
(2)媒体记者为了做好调查工作,决定从所随机抽取的市民中按年龄采用分层抽样的方法抽取20名接受采访,再从抽出的这20名中年龄在![]() 的选取2名担任主要发言人.记这2名主要发言人年龄在
的选取2名担任主要发言人.记这2名主要发言人年龄在![]() 的人数为
的人数为![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,某城市有一条公路正西方AO通过市中心O后转向北偏东α角方向的OB,位于该市的某大学M与市中心O的距离OM=3 ![]() km,且∠AOM=β,现要修筑一条铁路L,L在OA上设一站A,在OB上设一站B,铁路在AB部分为直线段,且经过大学M,其中tanα=2,cosβ=
km,且∠AOM=β,现要修筑一条铁路L,L在OA上设一站A,在OB上设一站B,铁路在AB部分为直线段,且经过大学M,其中tanα=2,cosβ= ![]() ,AO=15km.
,AO=15km. 
(1)求大学M在站A的距离AM;
(2)求铁路AB段的长AB.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在海岛![]() 上有一座海拔
上有一座海拔![]() 的山峰,山顶设有一个观察站
的山峰,山顶设有一个观察站![]() ,有一艘轮船按一固定方向做匀速直线航行,上午
,有一艘轮船按一固定方向做匀速直线航行,上午![]() 时,测得此船在岛北偏东
时,测得此船在岛北偏东![]() 、俯角为
、俯角为![]() 的
的![]() 处,到
处,到![]() 时,又测得该船在岛北偏西
时,又测得该船在岛北偏西![]() 、俯角
、俯角![]() 为的
为的![]() 处.
处.

(1)求船的航行速度;
(2)求船从![]() 到
到![]() 行驶过程中与观察站
行驶过程中与观察站![]() 的最短距离.
的最短距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数列{an}的前n项和为Sn,n∈N*.已知a1=1,a2=![]() ,a3=
,a3=![]() ,且当n≥2时,4Sn+2+5Sn=8Sn+1+Sn-1.
,且当n≥2时,4Sn+2+5Sn=8Sn+1+Sn-1.
(1)求a4的值;
(2)证明: ![]() 为等比数列.
为等比数列.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
, ![]() ,
, ![]() 为实数,
为实数, ![]() ,
, ![]() 为自然对数的底数,
为自然对数的底数, ![]() .
.
(1)当![]() ,
, ![]() 时,设函数
时,设函数![]() 的最小值为
的最小值为![]() ,求
,求![]() 的最大值;
的最大值;
(2)若关于![]() 的方程
的方程![]() 在区间
在区间![]() 上有两个不同实数解,求
上有两个不同实数解,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在△ABC中,已知|AB|=4 ![]() ,且三内角A,B,C满足2sin A+sin C=2sin B,建立适当的坐标系,求顶点C的轨迹方程.
,且三内角A,B,C满足2sin A+sin C=2sin B,建立适当的坐标系,求顶点C的轨迹方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com