
【题目】若点O在![]() 内,且满足
内,且满足![]() ,设
,设![]() 为
为![]() 的面积,
的面积, ![]() 为
为![]() 的面积,则
的面积,则![]() =________.
=________.
【答案】![]()
【解析】由![]() ,可得:
,可得: ![]()
延长OA,OB,OC,使OD=2OA,OE=4OB,OF=3OC,
如图所示:

∵2![]() +3
+3![]() +4
+4![]() =
=![]() ,
,
∴![]() ,
,
即O是△DEF的重心,
故△DOE,△EOF,△DOF的面积相等,
不妨令它们的面积均为1,
则△AOB的面积为![]() ,△BOC的面积为
,△BOC的面积为![]() ,△AOC的面积为
,△AOC的面积为![]() ,
,
故三角形△AOB,△BOC,△AOC的面积之比依次为: ![]() :
: ![]() :
: ![]() =3:2:4,
=3:2:4,
![]() .
.
故答案为: ![]() .
.
点睛:本题考查的知识点是三角形面积公式,三角形重心的性质,平面向量在几何中的应用,注意重要结论:点O在![]() 内,且满足
内,且满足![]() ,
, ![]() 则三角形△AOB,△BOC,△AOC的面积之比依次为:
则三角形△AOB,△BOC,△AOC的面积之比依次为: ![]() .
.
【题型】填空题
【结束】
16
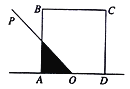
【题目】如图,正方形ABCD的边长为2,O为AD的中点,射线OP从OA出发,绕着点O顺时针方向旋转至OD,在旋转的过程中,记![]() 为
为![]() OP所经过的在正方形ABCD内的区域(阴影部分)的面积
OP所经过的在正方形ABCD内的区域(阴影部分)的面积![]() ,那么对于函数
,那么对于函数![]() 有以下三个结论:
有以下三个结论:
①![]() ;
;
②任意![]() ,都有
,都有![]() ;
;
③任意![]() 且
且![]() ,都有
,都有![]() .
.
其中正确结论的序号是__________. (把所有正确结论的序号都填上).
 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案 A加金题 系列答案
A加金题 系列答案科目:高中数学 来源: 题型:
【题目】如图,P是直线x=4上一动点,以P为圆心的圆Γ经定点B(1,0),直线l是圆Γ在点B处的切线,过A(﹣1,0)作圆Γ的两条切线分别与l交于E,F两点.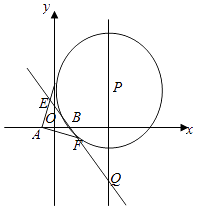
(1)求证:|EA|+|EB|为定值;
(2)设直线l交直线x=4于点Q,证明:|EB||FQ|=|BF|EQ|.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的前n项和为Sn,有2Sn=n2+n+4(n∈+)
(1)求数列的通项公式an;
(2)若bn= ,求数列{bn}的前n项和Tn.
,求数列{bn}的前n项和Tn.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,有两个独立的转盘(![]() )、(
)、(![]() ).两个图中三个扇形区域的圆心角分别为
).两个图中三个扇形区域的圆心角分别为![]() 、
、![]() 、
、![]() .用这两个转盘进行玩游戏,规则是:依次随机转动两个转盘再随机停下(指针固定不会动,当指针恰好落在分界线时,则这次结果无效,重新开始),记转盘(
.用这两个转盘进行玩游戏,规则是:依次随机转动两个转盘再随机停下(指针固定不会动,当指针恰好落在分界线时,则这次结果无效,重新开始),记转盘(![]() )指针所对的数为
)指针所对的数为![]() ,转盘(
,转盘(![]() )指针所对的数为
)指针所对的数为![]() ,(
,(![]() 、
、![]() ),求下列概率:
),求下列概率:

(1)![]() ;
;
(2)![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知关于x的一元二次函数![]() ,分别从集合
,分别从集合![]() 和
和![]() 中随机取一个数
中随机取一个数![]() 和
和![]() 得到数对
得到数对![]() .
.
(1)若![]() ,
, ![]() ,求函数
,求函数![]() 在
在![]() 内是偶函数的概率;
内是偶函数的概率;
(2)若![]() ,
, ![]() ,求函数
,求函数![]() 有零点的概率;
有零点的概率;
(3)若![]() ,
, ![]() ,求函数
,求函数![]() 在区间
在区间![]() 上是增函数的概率.
上是增函数的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】△ABC的内角A,B,C所对的边分别为a,b,c.向量 ![]() =(a,
=(a, ![]() b)与
b)与 ![]() =(cosA,sinB)平行.
=(cosA,sinB)平行.
(Ⅰ)求A;
(Ⅱ)若a= ![]() ,b=2,求△ABC的面积.
,b=2,求△ABC的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,某生态园将一三角形地块ABC的一角APQ开辟为水果园种植桃树,已知角A为120°,AB,AC的长度均大于200米,现在边界AP,AQ处建围墙,在PQ处围竹篱笆.
(1)若围墙AP,AQ总长度为200米,如何围可使得三角形地块APQ的面积最大?
(2)已知AP段围墙高1米,AQ段围墙高1.5米,AP段围墙造价为每平方米150元,AQ段围墙造价为每平方米100元.若围围墙用了30000元,问如何围可使竹篱笆用料最省?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=lnx+x2 .
(Ⅰ)求函数h(x)=f(x)﹣3x的极值;
(Ⅱ)若函数g(x)=f(x)﹣ax在定义域内为增函数,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知圆
中,已知圆![]() 的半径为2,圆心在
的半径为2,圆心在![]() 轴的正半轴上,且与直线
轴的正半轴上,且与直线![]() 相切.
相切.
(1)求圆![]() 的方程。
的方程。
(2)在圆![]() 上,是否存在点
上,是否存在点![]() ,使得直线
,使得直线![]() 与圆
与圆![]() 相交于不同的两点
相交于不同的两点![]() ,且△
,且△![]() 的面积最大?若存在,求出点
的面积最大?若存在,求出点![]() 的坐标及对应的△
的坐标及对应的△![]() 的面积;若不存在,请说明理由.
的面积;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com