
【题目】已知函数![]() ,关于
,关于![]() 的不等式
的不等式![]() 只有两个整数解,则实数
只有两个整数解,则实数![]() 的取值范围是( )
的取值范围是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】A
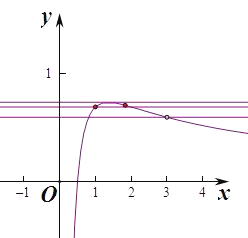
【解析】函数f(x)的定义域为(0,+∞),则![]() ,
,
当f′(x)>0得1ln(2x)>0,即ln(2x)<1,即0<2x<e,即![]() ,
,
由f′(x)<0得1ln(2x)<0,得ln(2x)>1,即2x>e,即![]() ,
,
即当![]() 时,函数f(x)取得极大值,同时也是最大值
时,函数f(x)取得极大值,同时也是最大值![]() ,
,
即当![]() 时,
时, ![]() 有一个整数解1,
有一个整数解1,
当![]() 时,
时, ![]() 有无数个整数解,
有无数个整数解,
若a=0,则f2(x)+af(x)>0得f2(x)>0,此时有无数个整数解,不满足条件。
若a>0,则由f2(x)+af(x)>0得f(x)>0或f(x)<a,
当f(x)>0时,不等式有无数个整数解,不满足条件。
当a<0时,由f2(x)+af(x)>0得f(x)>a或f(x)<0,
当f(x)<0时,没有整数解,
则要使当f(x)>a有两个整数解,
∵![]() ,
,
∴当f(x)ln2时,函数有两个整数点1,2,当![]() 时,函数有3个整数点1,2,3,
时,函数有3个整数点1,2,3,
∴要使f(x)>a有两个整数解,则![]() ,即
,即![]() ,
,
本题选择A选项.


 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案科目:高中数学 来源: 题型:
【题目】我市某机构为调查2017年下半年落实中学生“阳光体育”活动的情况,设平均每人每天参加体育锻炼时间为![]() (单位:分钟),按锻炼时间分下列四种情况统计:①0~10分钟;②11~20分钟;③21~30分钟;④30分钟以上,有10000名中学生参加了此项活动,图1是此次调查中某一项的流程图,其输出的结果是6400,则平均每天参加体育锻炼时间在0~20分钟内的学生的频率是( )
(单位:分钟),按锻炼时间分下列四种情况统计:①0~10分钟;②11~20分钟;③21~30分钟;④30分钟以上,有10000名中学生参加了此项活动,图1是此次调查中某一项的流程图,其输出的结果是6400,则平均每天参加体育锻炼时间在0~20分钟内的学生的频率是( )
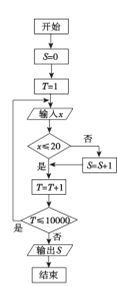
图1
A. 0.64 B. 0.36 C. 6400 D. 3600
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4 坐标系与参数方程
在直角坐标系![]() 中,圆
中,圆![]() ,曲线
,曲线![]() 的参数方程为
的参数方程为![]() 为参数),并以
为参数),并以![]() 为极点,
为极点, ![]() 轴正半轴为极轴建立极坐标系.
轴正半轴为极轴建立极坐标系.
(1)写出![]() 的极坐标方程,并将
的极坐标方程,并将![]() 化为普通方程;
化为普通方程;
(2)若直线![]() 的极坐标方程为
的极坐标方程为![]() 与
与![]() 相交于
相交于![]() 两点,
两点,
求![]() 的面积(
的面积(![]() 为圆
为圆![]() 的圆心).
的圆心).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,ABC为一直角三角形草坪,其中∠C=90°,BC=2米,AB=4米,为了重建草坪,设计师准备了两套方案: 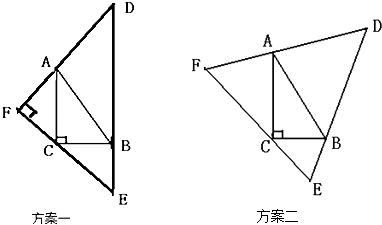
方案一:扩大为一个直角三角形,其中斜边DE过点B,且与AC平行,DF过点A,EF过点C;
方案二:扩大为一个等边三角形,其中DE过点B,DF过点A,EF过点C.
(1)求方案一中三角形DEF面积S1的最小值;
(2)求方案二中三角形DEF面积S2的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() (
(![]() 为自然对数的底数),
为自然对数的底数),![]() ,
, ![]() .
.
(1)若![]() ,且直线
,且直线![]() 分别与函数
分别与函数![]() 和
和![]() 的图象交于
的图象交于![]() ,求
,求![]() 两点间的最短距离;
两点间的最短距离;
(2)若![]() 时,函数
时,函数![]() 的图象恒在
的图象恒在![]() 的图象上方,求实数
的图象上方,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在学校体育节中,某班全体40名同学参加跳绳、踢毽子两项比赛的人数统计如下:
参加跳绳的同学 | 未参加跳绳的同学 | |
参加踢毽的同学 | 9 | 4 |
未参加踢毽的同学 | 7 | 20 |
(1)从该班随机选1名同学,求该同学至少参加上述一项活动的概率;
(2)已知既参加跳绳又参加踢毽的9名同学中,有男生5名,女生4名,现从这5名男生,4名女生中各随机挑选1人,求男同学甲未被选中且女同学乙被选中的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com