
【题目】下列四个函数:①y=3﹣x;② ![]() ;③y=x2+2x﹣10;④
;③y=x2+2x﹣10;④  ,其中值域为R的函数有( )
,其中值域为R的函数有( )
A.1个
B.2个
C.3个
D.4个
【答案】B
【解析】解:根据一次函数的值域为R,y=3﹣x为一次函数,故①满足条件;
根据x2+1≥1,可得 ![]() ,即函数
,即函数 ![]() 的值域为(0,1],故②不满足条件;
的值域为(0,1],故②不满足条件;
二次函数y=x2+2x﹣10的最小值为﹣11,无最大值,故函数y=x2+2x﹣10的值域为[﹣11,+∞),故③不满足条件;
当x≤0时,y=﹣x≥0,当x>0时,y=﹣ ![]() <0,故函数
<0,故函数 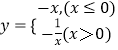 的值域为R,故④满足条件;
的值域为R,故④满足条件;
故选B
【考点精析】解答此题的关键在于理解函数的值域的相关知识,掌握求函数值域的方法和求函数最值的常用方法基本上是相同的.事实上,如果在函数的值域中存在一个最小(大)数,这个数就是函数的最小(大)值.因此求函数的最值与值域,其实质是相同的.


科目:高中数学 来源: 题型:
【题目】给出下列函数:①f(x)= ![]() ,g(x)=x+1;②f(x)=|x|,g(x)=
,g(x)=x+1;②f(x)=|x|,g(x)= ![]() ;③f(x)=x2﹣2x﹣1,g(t)=t2﹣2t﹣1.其中,是同一函数的是( )
;③f(x)=x2﹣2x﹣1,g(t)=t2﹣2t﹣1.其中,是同一函数的是( )
A.①②③
B.①③
C.②③
D.②
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在定义域内给定区间[a,b]上存在x0(a<x0<b)满足f(x0)= ![]() ,则称函数y=f(x)在区间[a,b]上的“平均值函数”,x0是它的一个均值点.若函数f(x)=﹣x2+mx+1是[﹣1,1]上的平均值函数,则实数m的取值范围是
,则称函数y=f(x)在区间[a,b]上的“平均值函数”,x0是它的一个均值点.若函数f(x)=﹣x2+mx+1是[﹣1,1]上的平均值函数,则实数m的取值范围是
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义在R的奇函数f(x)满足当x>0时,f(x)=|2x﹣2|, 
(1)求函数f(x)的解析式;
(2)在图中的坐标系中作出函数y=f(x)的图象,并找出函数的单调区间;
(3)若集合{x|f(x)=a}恰有两个元素,结合函数f(x)的图象求实数a应满足的条件.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题中正确的有( )
①命题x∈R,使sin x+cos x= ![]() 的否定是“对x∈R,恒有sin x+cos x≠
的否定是“对x∈R,恒有sin x+cos x≠ ![]() ”;
”;
②“a≠1或b≠2”是“a+b≠3”的充要条件;
③若曲线C上的所有点的坐标都满足方程f(x,y)=0,则称方程f(x,y)=0是曲线C的方程;
④十进制数66化为二进制数是1 000 010(2) .
A.①②③④
B.①④
C.②③
D.③④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图.已知等腰梯形ABCD中,AB∥CD,AD=AB=![]() CD,M是的CD的中点.N是AC与BM的交点,将△BCM沿BM向上翻折成△BPM,使平面BPM⊥平面ABMD
CD,M是的CD的中点.N是AC与BM的交点,将△BCM沿BM向上翻折成△BPM,使平面BPM⊥平面ABMD
(I)求证:AB⊥PN.
(Ⅱ)若E为PA的中点.求证:EN∥平面PDM.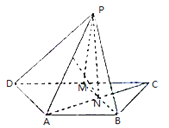
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com