
【题目】如图1,∠ACB=45°,BC=3,过动点A作AD⊥BC,垂足D在线段BC上且异于点B,连接AB,沿AD将△ABD折起,使∠BDC=90°(如图2所示),
(1)当BD的长为多少时,三棱锥A﹣BCD的体积最大;
(2)当三棱锥A﹣BCD的体积最大时,设点E,M分别为棱BC,AC的中点,试在棱CD上确定一点N,使得EN⊥BM,并求EN与平面BMN所成角的大小.
【答案】
(1)解:设BD=x,则CD=3﹣x
∵∠ACB=45°,AD⊥BC,∴AD=CD=3﹣x
∵折起前AD⊥BC,∴折起后AD⊥BD,AD⊥CD,BD∩DC=D
∴AD⊥平面BCD
∴VA﹣BCD= ![]() ×AD×S△BCD=
×AD×S△BCD= ![]() ×(3﹣x)×
×(3﹣x)× ![]() ×x(3﹣x)=
×x(3﹣x)= ![]() (x3﹣6x2+9x)
(x3﹣6x2+9x)
设f(x)= ![]() (x3﹣6x2+9x) x∈(0,3),
(x3﹣6x2+9x) x∈(0,3),
∵f′(x)= ![]() (x﹣1)(x﹣3),∴f(x)在(0,1)上为增函数,在(1,3)上为减函数
(x﹣1)(x﹣3),∴f(x)在(0,1)上为增函数,在(1,3)上为减函数
∴当x=1时,函数f(x)取最大值
∴当BD=1时,三棱锥A﹣BCD的体积最大
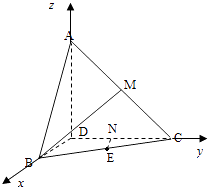
(2)解:以D为原点,建立如图直角坐标系D﹣xyz,
由(1)知,三棱锥A﹣BCD的体积最大时,BD=1,AD=CD=2
∴D(0,0,0),B(1,0,0),C(0,2,0),A(0,0,2),M(0,1,1),E( ![]() ,1,0),且
,1,0),且 ![]() =(﹣1,1,1)
=(﹣1,1,1)
设N(0,λ,0),则 ![]() =(﹣
=(﹣ ![]() ,λ﹣1,0)
,λ﹣1,0)
∵EN⊥BM,∴ ![]()
![]() =0
=0
即(﹣1,1,1)(﹣ ![]() ,λ﹣1,0)=
,λ﹣1,0)= ![]() +λ﹣1=0,∴λ=
+λ﹣1=0,∴λ= ![]() ,∴N(0,
,∴N(0, ![]() ,0)
,0)
∴当DN= ![]() 时,EN⊥BM
时,EN⊥BM
设平面BMN的一个法向量为 ![]() =(x,y,z),由
=(x,y,z),由 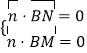 及
及 ![]() =(﹣1,
=(﹣1, ![]() ,0)
,0)
得 ![]() ,取
,取 ![]() =(1,2,﹣1)
=(1,2,﹣1)
设EN与平面BMN所成角为θ,则 ![]() =(﹣
=(﹣ ![]() ,﹣
,﹣ ![]() ,0)
,0)
sinθ=|cos< ![]() ,
, ![]() >|=|
>|=| ![]() |=
|= ![]() =
= ![]()
∴θ=60°
∴EN与平面BMN所成角的大小为60°
【解析】(1)设BD=x,先利用线面垂直的判定定理证明AD即为三棱锥A﹣BCD的高,再将三棱锥的体积表示为x的函数,最后利用导数求函数的最大值即可;(2)由(1)可先建立空间直角坐标系,写出相关点的坐标和相关向量的坐标,设出动点N的坐标,先利用线线垂直的充要条件计算出N点坐标,从而确定N点位置,再求平面BMN的法向量,从而利用夹角公式即可求得所求线面角


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),在以原点为极点,
为参数),在以原点为极点, ![]() 轴正半轴为极轴的极坐标系中,直线
轴正半轴为极轴的极坐标系中,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的普通方程和直线
的普通方程和直线![]() 的倾斜角;
的倾斜角;
(2)设点![]() ,直线
,直线![]() 和曲线
和曲线![]() 交于
交于![]() 两点,求
两点,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】购买一件售价为5 000元的商品,采用分期付款的办法,每期付款数相同,购买后1个月付款一次,过1个月再付款一次,如此下去,到第12次付款后全部付清.如果月利率为0.8%,每月利息按复利计算(上月利息计入下月本金),那么每期应付款多少元?(精确到1元)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某海上养殖基地A,接到气象部门预报,位于基地南偏东60°方向相距20(![]() +1)海里的海面上有一台风中心,影响半径为20海里,正以每小时10
+1)海里的海面上有一台风中心,影响半径为20海里,正以每小时10![]() 海里的速度沿某一方向匀速直线前进,预计台风中心在基地东北方向时对基地的影响最强烈且(
海里的速度沿某一方向匀速直线前进,预计台风中心在基地东北方向时对基地的影响最强烈且(![]() +1)小时后开始影响基地持续2小时,求台风移动的方向.
+1)小时后开始影响基地持续2小时,求台风移动的方向.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,ABCD为矩形,PA⊥平面ABCD,PA=AD,M,N,Q分别是PC,AB,CD的中点.

求证:(1)MN∥平面PAD;
(2)平面QMN∥平面PAD.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数y=f(x﹣1)的图象关于直线x=1对称,且当x∈(﹣∞,0)时,f(x)+xf′(x)<0成立若a=(20.2)f(20.2),b=(1n2)f(1n2),c=( ![]() )f(
)f( ![]() ),则a,b,c的大小关系是( )
),则a,b,c的大小关系是( )
A.a>b>c
B.b>a>c
C.c>a>b
D.a>c>b
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() 分别为椭圆
分别为椭圆![]() 的左、右焦点,点
的左、右焦点,点![]() 为椭圆
为椭圆![]() 的左顶点,点
的左顶点,点![]() 为椭圆
为椭圆![]() 的上顶点,且
的上顶点,且![]() .
.
(1)若椭圆![]() 的离心率为
的离心率为![]() ,求椭圆
,求椭圆![]() 的方程;
的方程;
(2)设![]() 为椭圆
为椭圆![]() 上一点,且在第一象限内,直线
上一点,且在第一象限内,直线![]() 与
与![]() 轴相交于点
轴相交于点![]() ,若以
,若以![]() 为直径的圆经过点
为直径的圆经过点![]() ,证明:点
,证明:点![]() 在直线
在直线![]() 上.
上.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系xoy中,已知椭圆C: ![]() =1(a>b>0)的离心率e=
=1(a>b>0)的离心率e= ![]() ,左顶点为A(﹣4,0),过点A作斜率为k(k≠0)的直线l交椭圆C于点D,交y轴于点E.
,左顶点为A(﹣4,0),过点A作斜率为k(k≠0)的直线l交椭圆C于点D,交y轴于点E. 
(1)求椭圆C的方程;
(2)已知P为AD的中点,是否存在定点Q,对于任意的k(k≠0)都有OP⊥EQ,若存在,求出点Q的坐标;若不存在说明理由;
(3)若过O点作直线l的平行线交椭圆C于点M,求 ![]() 的最小值.
的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com