
 是等差数列;
是等差数列;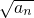 是等差数列,并说明理由.
是等差数列,并说明理由.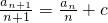 ,即
,即 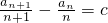
 }是首项为1,公差为c的等差数列
}是首项为1,公差为c的等差数列 =1+(n-1)c,即an=cn2+(1-c)n
=1+(n-1)c,即an=cn2+(1-c)n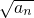 是等差数列的充要条件是
是等差数列的充要条件是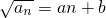
 ,又p+q≥3
,又p+q≥3 (k∈N且k≥3).
(k∈N且k≥3).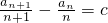 ,然后根据等差数列的定义进行判定即可;
,然后根据等差数列的定义进行判定即可;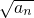 是等差数列的充要条件是
是等差数列的充要条件是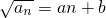 ,然后化简变形可求出c的值;
,然后化简变形可求出c的值;

 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案科目:高中数学 来源: 题型:
| 3+4an |
| 12-4an |
| 1 | ||
an-
|
查看答案和解析>>
科目:高中数学 来源: 题型:
| 3 |
| 2 |
| 3nan-1 |
| 2an-1+n-1 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 5 | 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com