解:(1)∵a
n+1-a
n=3,
∴b
n+1-b
n=n+2,
∵b
1=1,
∴b
2=4,b
3=8.
(2)∵
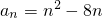
.
∴a
n+1-a
n=2n-7,
∴b
n+1-b
n=
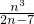
,
由b
n+1-b
n>0,解得n≥4,即b
4<b
5<b
6…;
由b
n+1-b
n<0,解得n≤3,即b
1>b
2>b
3>b
4.
∴k=4.
(3)∵a
n+1-a
n=(-1)
n+1,
∴b
n+1-b
n=(-1)
n+1(2
n+n).
∴b
n-b
n-1=(-1)
n(2
n-1+n-1)(n≥2).
故b
2-b
1=2
1+1;
b
3-b
2=(-1)(2
2+2),
…
b
n-1-b
n-2=(-1)
n-1(2
n-2+n-2).
b
n-b
n-1=(-1)
n(2
n-1+n-1).
当n=2k时,以上各式相加得
b
n-b
1=(2-2
2+…-2
n-2+2
n-1)+[1-2+…-(n-2)+(n-1)]
=
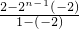
+

=
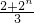
+

.
∴b
n=
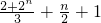
=

+

+

.
当n=2k-1时,
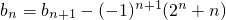
=
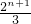
+

+

-(2
n+n)
=-

-

+

∴b
n=
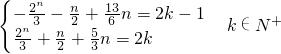
.
分析:(1)先根据条件得到数列{b
n}的递推关系式,即可求出结论;
(2)先根据条件得到数列{b
n}的递推关系式;进而判断出其增减性,即可求出结论;
(3)先根据条件得到数列{b
n}的递推关系式;再结合叠加法以及分类讨论分情况求出数列{b
n}的通项公式,最后综合即可.
点评:本题主要考察数列递推关系式在求解数列通项中的应用.是对数列知识的综合考察,属于难度较高的题目.

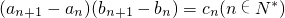 .
.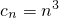 ,
,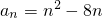 .求正整数k,使得对一切n∈N*,均有bn≥bk;
.求正整数k,使得对一切n∈N*,均有bn≥bk;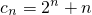 ,
,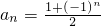 .当b1=1时,求数列{bn}的通项公式.
.当b1=1时,求数列{bn}的通项公式.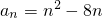 .
.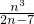 ,
,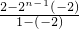 +
+ =
=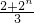 +
+ .
.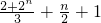 =
= +
+ +
+ .
.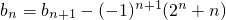
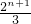 +
+ +
+ -(2n+n)
-(2n+n) -
- +
+
 .
.
