【题目】在△ABC中，角A，B，C的对边分别是a，b，c，点（a，b）在4xcosB﹣ycosC=ccosB上．
（1）cosB的值；
（2）若 
=3，b=3 
，求a和c．
【答案】
（1）解：由题意得4acosB﹣bcosC=ccosB，
由正弦定理得4sinAcosB﹣sinBcosC=sinCcosB，
整理得4sinAcosB=sin（B+C）=sinA，
∵sinA≠0，
∴cosB= 
．
（2）解： 
=| || |cosB= ac=3，
∴ac=12，由b2=a2+c2﹣2accosB，
∴a2+c2=24，
∴a2+c2﹣2ac=（a﹣c）2=0，
∴a=c，
∴a=c=2 
【解析】（1）由正弦定理把已知等式中的边转化为角的正弦，利用两角和公式化简即可求得cosB的值．（2）利用向量的数量积的运算求得ac的值，进而利用余弦定理求得a2+c2的值，进而联立方程求得a和c．
【考点精析】通过灵活运用正弦定理的定义和余弦定理的定义，掌握正弦定理:
；余弦定理:
;
;
即可以解答此题．
科目：高中数学 来源： 题型：
【题目】已知f（x）为一次函数，g（x）为二次函数，且f[g（x）]=g[f（x）]．
（1）求f（x）的解析式；
（2）若y=g（x）与x轴及y=f（x）都相切，且g（0）=
，求g（x）的解析式．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】函数f（x）=sinωx（＞0）的图象向右平移 
个单位得到函数y=g（x）的图象，并且函数g（x）在区间[ 
， 
]上单调递增，在区间[ 
]上单调递减，则实数ω的值为（ ）
A.
B.
C.2
D.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某自行车厂为共享单车公司生产新样式的单车，已知生产新样式单车的固定成本为20000元，每生产一件新样式单车需要增加投入100元．根据初步测算，自行车厂的总收益（单位：元）满足分段函数h（x），其中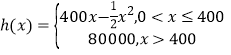
,x是新样式单车的月产量（单位：件），利润=总收益﹣总成本．
（1）试将自行车厂的利润y元表示为月产量x的函数；
（2）当月产量为多少件时自行车厂的利润最大？最大利润是多少？
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知关于x的不等式|x﹣3|+|x﹣m|≥2m的解集为R． （Ⅰ）求m的最大值；
（Ⅱ）已知a＞0，b＞0，c＞0，且a+b+c=m，求4a2+9b2+c2的最小值及此时a，b，c的值．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数f（x）=loga（1+x），g（x）=loga（1﹣x），（a＞1）．
（1）求函数h(x)=f（x）﹣g（x）的定义域；
（2）求使f（x）﹣g（x）＞0的x的取值范围．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知椭圆
的离心率e＝
，连接椭圆的四个顶点得到的菱形的面积为4.
(1)求椭圆的方程；
(2)设直线
过椭圆的左端点A，与椭圆的另一个交点为B.，AB的垂直平分线交
轴于点
，且
·
＝4，求
的值．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数
．
（1）若f（﹣1）=﹣3，求a
（2）若f（x）的定义域为R，求a的取值范围；
（3）是否存在实数a，使f（x）在（﹣∞，2）上为增函数？若存在，求出a的范围？若不存在，说明理由．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com