
ЁОЬтФПЁПЁЖГЧЪаЙцЛЎЙмРэвтМћЁЗРяУцЬсГіЁАаТНЈзЁеЌвЊЭЦЙуНжЧјжЦЃЌддђЩЯВЛдйНЈЩшЗтБезЁеЌаЁЧјЃЌвбНЈГЩЕФЗтБеаЁЧјКЭЕЅЮЛДѓдКвЊж№ВНДђПЊЁБЃЌетИіЯћЯЂдкЭјЩЯвЛЪЏМЄЦ№ЧЇВуРЫЃЌИїжжЫЕЗЈВЛвЛЖјзу.ФГЭјеОЮЊСЫНтОгУёЖдЁАПЊЗХаЁЧјЁБШЯЭЌгыЗёЃЌДг![]() ЫъЕФШЫШКжаЫцЛњГщШЁСЫ
ЫъЕФШЫШКжаЫцЛњГщШЁСЫ![]() ШЫНјааЮЪОэЕїВщЃЌВЂЧвзіГіСЫИїИіФъСфЖЮЕФЦЕТЪЗжВМжБЗНЭМЃЈВПЗжЃЉШчЭМЫљЪОЃЌЭЌЪБЖд
ШЫНјааЮЪОэЕїВщЃЌВЂЧвзіГіСЫИїИіФъСфЖЮЕФЦЕТЪЗжВМжБЗНЭМЃЈВПЗжЃЉШчЭМЫљЪОЃЌЭЌЪБЖд![]() ШЫЖдетЁАПЊЗХаЁЧјЁБШЯЭЌЧщПіНјааЭГМЦЕУЕНЯТБэЃК
ШЫЖдетЁАПЊЗХаЁЧјЁБШЯЭЌЧщПіНјааЭГМЦЕУЕНЯТБэЃК

ЃЈЂёЃЉЭъГЩЫљИјЕФЦЕТЪЗжВМжБЗНЭМЃЌВЂЧѓ![]() ЕФжЕЃЛ
ЕФжЕЃЛ
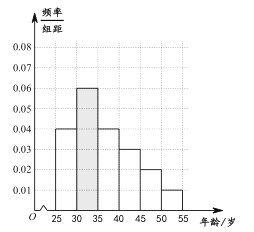
ЃЈЂђЃЉШчЙћДг![]() СНИіФъСфЖЮжаЕФЁАШЯЭЌЁБШЫШКжаЃЌАДЗжВуГщбљЕФЗНЗЈГщШЁ6ШЫВЮгызљЬИЛсЃЌШЛКѓДгет6ШЫжаЫцЛњГщШЁ2ШЫзїНјвЛВНЕїВщЃЌЧѓет2ШЫЕФФъСфЖМдк
СНИіФъСфЖЮжаЕФЁАШЯЭЌЁБШЫШКжаЃЌАДЗжВуГщбљЕФЗНЗЈГщШЁ6ШЫВЮгызљЬИЛсЃЌШЛКѓДгет6ШЫжаЫцЛњГщШЁ2ШЫзїНјвЛВНЕїВщЃЌЧѓет2ШЫЕФФъСфЖМдк![]() ФкЕФИХТЪ .
ФкЕФИХТЪ .
ЁОД№АИЁПЃЈ1ЃЉ60ЃЛЃЈ2ЃЉ![]()
ЁОНтЮіЁПЗжЮіЃКЃЈ1ЃЉИљОнжБЗНЭМжаЃЌУПИіаЁОиаЮЕФУцЛ§КЭЮЊ![]() ЃЌПЩЕУЕкЖўзщОиаЮЕФЦЕТЪЃЌГ§вдзщОрПЩЕУЦЕТЪЗжВМжБЗНЭМжаЕкЖўзщОиаЮЕФИпЃЌДгЖјПЩЕУЭъећЕФжБЗНЭМЃЌИљОнжБЗНЭМгыБэИёжаЪ§ОнПЩЕУ
ЃЌПЩЕУЕкЖўзщОиаЮЕФЦЕТЪЃЌГ§вдзщОрПЩЕУЦЕТЪЗжВМжБЗНЭМжаЕкЖўзщОиаЮЕФИпЃЌДгЖјПЩЕУЭъећЕФжБЗНЭМЃЌИљОнжБЗНЭМгыБэИёжаЪ§ОнПЩЕУ![]() ЕФжЕЃЛгЩЃЈ1ЃЉжЊЃК
ЕФжЕЃЛгЩЃЈ1ЃЉжЊЃК![]() СНИіФъСфЖЮжаЕФЁАШЯЭЌЁБШЫЪ§ЗжБ№ЮЊ
СНИіФъСфЖЮжаЕФЁАШЯЭЌЁБШЫЪ§ЗжБ№ЮЊ![]() ШЫЃЌ
ШЫЃЌ![]() ШЫЃЌвђДЫАДееЗжВуГщбљГщШЁ6ШЫЪБЃЌСНИіФъСфЖЮЕФШЫЪ§ЗжБ№ЮЊ4ШЫЃЌ2ШЫЃЌгЩЙХЕфИХаЭИХТЪЙЋЪНПЩЕУНсЙћ.
ШЫЃЌвђДЫАДееЗжВуГщбљГщШЁ6ШЫЪБЃЌСНИіФъСфЖЮЕФШЫЪ§ЗжБ№ЮЊ4ШЫЃЌ2ШЫЃЌгЩЙХЕфИХаЭИХТЪЙЋЪНПЩЕУНсЙћ.
ЯъНтЃКЃЈ1ЃЉгЩЬтвтжЊЃКЕкЖўзщЕФЦЕТЪЮЊ![]() .
.
ЫљвдЃЌЦЕТЪЗжВМжБЗНЭМжаЕкЖўзщЫљЪООиаЮЕФИпЮЊ![]() ЃЌ
ЃЌ
ВЙГфКѓЕФЦЕТЪЗжВМжБЗНЭМШчЭМЫљЪО.
ЕквЛзщШЫЪ§ЮЊ![]() ШЫЃЌЦЕТЪЮЊ
ШЫЃЌЦЕТЪЮЊ![]() ЃЌдђ
ЃЌдђ![]() ШЫ.
ШЫ.
ЕкЖўзщШЫЪ§ЮЊ![]() ШЫЃЌ
ШЫЃЌ![]()
ЕкЫФзщШЫЪ§ЮЊ![]() ШЫЃЌШЯЭЌШЫЪ§
ШЫЃЌШЯЭЌШЫЪ§![]() ШЫ.
ШЫ.
ЃЈ2ЃЉгЩЃЈ1ЃЉжЊЃК![]() СНИіФъСфЖЮжаЕФЁАШЯЭЌЁБШЫЪ§ЗжБ№ЮЊ
СНИіФъСфЖЮжаЕФЁАШЯЭЌЁБШЫЪ§ЗжБ№ЮЊ![]() ШЫЃЌ
ШЫЃЌ![]() ШЫЃЌвђДЫАДееЗжВуГщбљГщШЁ6ШЫЪБЃЌСНИіФъСфЖЮЕФШЫЪ§ЗжБ№ЮЊ4ШЫЃЌ2ШЫЃЌвђДЫЫљЧѓИХТЪЮЊ
ШЫЃЌвђДЫАДееЗжВуГщбљГщШЁ6ШЫЪБЃЌСНИіФъСфЖЮЕФШЫЪ§ЗжБ№ЮЊ4ШЫЃЌ2ШЫЃЌвђДЫЫљЧѓИХТЪЮЊ![]() .
.


 гХМгОЋОэЯЕСаД№АИ
гХМгОЋОэЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЂйЯпадЛиЙщЗНГЬЖдгІЕФжБЯп![]() жСЩйОЙ§ЦфбљБОЪ§ОнЕу
жСЩйОЙ§ЦфбљБОЪ§ОнЕу![]() жаЕФвЛИіЕуЃЛ
жаЕФвЛИіЕуЃЛ
ЂкШєСНИіБфСПЕФЯпадЯрЙиаддНЧПЃЌдђЯрЙиЯЕЪ§ЕФОјЖджЕдННгНќгк![]() ЃЛ
ЃЛ
ЂлдкФГЯюВтСПжаЃЌВтСПНсЙћ![]() ЗўДге§ЬЌЗжВМ
ЗўДге§ЬЌЗжВМ![]()
![]() ЃЌШє
ЃЌШє![]() ЮЛгкЧјгђ
ЮЛгкЧјгђ![]() ФкЕФИХТЪЮЊ
ФкЕФИХТЪЮЊ![]() ЃЌдђ
ЃЌдђ![]() ЮЛгкЧјгђ
ЮЛгкЧјгђ![]() ФкЕФИХТЪЮЊ
ФкЕФИХТЪЮЊ![]() ЃЛ
ЃЛ
ЂмЖдЗжРрБфСП![]() гы
гы![]() ЕФЫцЛњБфСПK2ЕФЙлВтжЕkРДЫЕЃЌkдНаЁЃЌХаЖЯЁА
ЕФЫцЛњБфСПK2ЕФЙлВтжЕkРДЫЕЃЌkдНаЁЃЌХаЖЯЁА![]() гы
гы![]() гаЙиЯЕЁБЕФАбЮедНДѓЃЎЦфжаецУќЬтЕФађКХЮЊ( )
гаЙиЯЕЁБЕФАбЮедНДѓЃЎЦфжаецУќЬтЕФађКХЮЊ( )
A. ЂйЂм B. ЂкЂм C. ЂйЂл D. ЂкЂл
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊКЏЪ§![]() ЃЈ
ЃЈ![]() ЃЌ
ЃЌ ![]() ЮЊздШЛЖдЪ§ЕФЕзЪ§ЃЉЃЌЧвЧњЯп
ЮЊздШЛЖдЪ§ЕФЕзЪ§ЃЉЃЌЧвЧњЯп![]() дкЕу
дкЕу![]() ДІЕФЧаЯпЦНаагк
ДІЕФЧаЯпЦНаагк![]() жс.
жс.
ЃЈ1ЃЉЧѓ![]() ЕФжЕЃЛ
ЕФжЕЃЛ
ЃЈ2ЃЉЧѓКЏЪ§![]() ЕФМЋжЕ.
ЕФМЋжЕ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊМЏКЯA={x|x2Љ2xЉ3Ём0ЃЌxЁЪR}ЃЌB={x|mЉ1ЁмxЁмm+1ЃЌxЁЪRЃЌmЁЪR}
ЃЈ1ЃЉШєAЁЩB=[1ЃЌ3]ЃЌЧѓЪЕЪ§mЕФжЕЃЛ
ЃЈ2ЃЉШєARBЃЌЧѓЪЕЪ§mЕФШЁжЕЗЖЮЇЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкЦНУцжБНЧзјБъЯЕжаЃЌдВ![]() ЕФЗНГЬЮЊ
ЕФЗНГЬЮЊ![]() ЃЈ
ЃЈ![]() ЮЊВЮЪ§ЃЉЃЎвдзјБъдЕуЮЊМЋЕуЃЌ
ЮЊВЮЪ§ЃЉЃЎвдзјБъдЕуЮЊМЋЕуЃЌ![]() жсЕФе§АыжсЮЊМЋжсЃЌНЈСЂМЋзјБъЯЕЃЌСНжжзјБъЯЕжаШЁЯрЭЌЕФЕЅЮЛГЄЖШЃЌжБЯп
жсЕФе§АыжсЮЊМЋжсЃЌНЈСЂМЋзјБъЯЕЃЌСНжжзјБъЯЕжаШЁЯрЭЌЕФЕЅЮЛГЄЖШЃЌжБЯп![]() ЕФМЋзјБъЗНГЬЮЊ
ЕФМЋзјБъЗНГЬЮЊ![]()
ЃЈ1ЃЉЕБ![]() ЪБЃЌХаЖЯжБЯп
ЪБЃЌХаЖЯжБЯп![]() гыдВ
гыдВ![]() ЕФЙиЯЕЃЛ
ЕФЙиЯЕЃЛ
ЃЈ2ЃЉЕБ![]() ЩЯгаЧвжЛгавЛЕуЕНжБЯп
ЩЯгаЧвжЛгавЛЕуЕНжБЯп![]() ЕФОрРыЕШгк
ЕФОрРыЕШгк![]() ЪБЃЌЧѓ
ЪБЃЌЧѓ![]() ЩЯЕНжБЯп
ЩЯЕНжБЯп![]() ОрРыЮЊ
ОрРыЮЊ![]() ЕФЕуЕФзјБъЃЎ
ЕФЕуЕФзјБъЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЭждВ![]() ЃК
ЃК ![]() ЕФзѓгвНЙЕуЗжБ№ЮЊ
ЕФзѓгвНЙЕуЗжБ№ЮЊ![]() ЃЌ
ЃЌ ![]() ЃЌзѓЖЅЕуЮЊ
ЃЌзѓЖЅЕуЮЊ![]() ЃЌЩЯЖЅЕуЮЊ
ЃЌЩЯЖЅЕуЮЊ![]() ЃЌ
ЃЌ ![]() ЕФУцЛ§ЮЊ
ЕФУцЛ§ЮЊ![]() .
.
ЃЈ1ЃЉЧѓЭждВ![]() ЕФЗНГЬЃЛ
ЕФЗНГЬЃЛ
ЃЈ2ЃЉЩшжБЯп![]() ЃК
ЃК ![]() гыЭждВ
гыЭждВ![]() ЯрНЛгкВЛЭЌЕФСНЕу
ЯрНЛгкВЛЭЌЕФСНЕу![]() ЃЌ
ЃЌ ![]() ЃЌ
ЃЌ ![]() ЪЧЯпЖЮ
ЪЧЯпЖЮ![]() ЕФжаЕу.ШєОЙ§Еу
ЕФжаЕу.ШєОЙ§Еу![]() ЕФжБЯп
ЕФжБЯп![]() гыжБЯп
гыжБЯп![]() ДЙжБгкЕу
ДЙжБгкЕу![]() ЃЌЧѓ
ЃЌЧѓ![]() ЕФШЁжЕЗЖЮЇ.
ЕФШЁжЕЗЖЮЇ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЯђСП ![]() ЃЌШєfЃЈxЃЉ=mnЃЎ ЃЈIЃЉЧѓfЃЈxЃЉЕФЕЅЕїЕндіЧјМфЃЛ
ЃЌШєfЃЈxЃЉ=mnЃЎ ЃЈIЃЉЧѓfЃЈxЃЉЕФЕЅЕїЕндіЧјМфЃЛ
ЃЈIIЃЉМКжЊЁїABCЕФШ§ФкНЧAЃЌBЃЌCЖдБпЗжБ№ЮЊaЃЌbЃЌcЃЌЧвa=3ЃЌf ![]() ЃЌsinC=2sinBЃЌЧѓAЃЌcЃЌbЕФжЕЃЎ
ЃЌsinC=2sinBЃЌЧѓAЃЌcЃЌbЕФжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊКЏЪ§fЃЈxЃЉ=xЃЈlnxЉ2axЃЉгаСНИіМЋжЕЕуЃЌдђЪЕЪ§aЕФШЁжЕЗЖЮЇЪЧЃЈ ЃЉ
A.ЃЈЉЁоЃЌ ![]() ЃЉ
ЃЉ
B.ЃЈ0ЃЌ ![]() ЃЉ
ЃЉ
C.ЃЈ0ЃЌ ![]() ЃЉ
ЃЉ
D.ЃЈ ![]() ЃЌ+ЁоЃЉ
ЃЌ+ЁоЃЉ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЯжга![]() ИіаЁЧђЃЌМзЁЂввСНЮЛЭЌбЇТжСїЧвВЛЗХЛизЅЧђЃЌУПДЮзюЩйзЅ1ИіЧђЃЌзюЖрзЅ3ИіЧђЃЌЙцЖЈЫзЅЕНзюКѓвЛИіЧђЫгЎ. ШчЙћМзЯШзЅЃЌФЧУДЯТСаЭЦЖЯе§ШЗЕФЪЧЃЈ ЃЉ
ИіаЁЧђЃЌМзЁЂввСНЮЛЭЌбЇТжСїЧвВЛЗХЛизЅЧђЃЌУПДЮзюЩйзЅ1ИіЧђЃЌзюЖрзЅ3ИіЧђЃЌЙцЖЈЫзЅЕНзюКѓвЛИіЧђЫгЎ. ШчЙћМзЯШзЅЃЌФЧУДЯТСаЭЦЖЯе§ШЗЕФЪЧЃЈ ЃЉ
A. Шє![]() =4ЃЌдђМзгаБигЎЕФВпТд B. Шє
=4ЃЌдђМзгаБигЎЕФВпТд B. Шє![]() =6ЃЌдђввгаБигЎЕФВпТд
=6ЃЌдђввгаБигЎЕФВпТд
C. Шє![]() =9ЃЌдђМзгаБигЎЕФВпТд D. Шє
=9ЃЌдђМзгаБигЎЕФВпТд D. Шє![]() =11ЃЌдђввгаБигЎЕФВпТд
=11ЃЌдђввгаБигЎЕФВпТд
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com