
【题目】已知椭圆C:![]() 1(a>b>0)过A(2,0),B(0,1)两点.
1(a>b>0)过A(2,0),B(0,1)两点.
(1)求椭圆C的方程和离心率的大小;
(2)设M,N是y轴上不同的两点,若两点的纵坐标互为倒数,直线AM与椭圆C的另一个交点为P,直线AN与椭圆C的另一个交点为Q,判断直线PQ与x轴的位置关系,并证明你的结论.
【答案】(1)![]() ;离心率
;离心率![]() (2)直线PQ与x轴平行;证明见解析
(2)直线PQ与x轴平行;证明见解析
【解析】
(1)依题意得a=2,b=1,写出椭圆C的方程,求解离心率的大小即可.
(2)设M,N坐标为(0,m),(0,n),则![]() ,m≠0,n≠0,由A(2,0),M(0,m)得直线AM的方程为
,m≠0,n≠0,由A(2,0),M(0,m)得直线AM的方程为![]() ,联立
,联立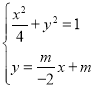 ,求出P的纵坐标,Q纵坐标,然后推出结果.
,求出P的纵坐标,Q纵坐标,然后推出结果.
解法二:设直线AM的方程为x=ty+2(t≠0),直线AN的方程为x=sy+2(s≠0)令x=0得tyM=﹣2,M坐标为![]() ,同理N坐标为
,同理N坐标为![]() ,推出yP=yQ≠0,直线PQ与x轴平行.
,推出yP=yQ≠0,直线PQ与x轴平行.
解法三:设直线AM的方程为y=k1(x﹣2),k1≠0,直线AN的方程为y=k2(x﹣2),k2≠0,令x=0得M坐标为(0,﹣2k1),同理N坐标为(0,﹣2k2),得到4k1k2=1,代入椭圆方程求出P的纵坐标,Q的纵坐标,即可得到结果.
(1)依题意得a=2,b=1,所以椭圆C的方程为![]() ,
,![]() ,
,
离心率的大小![]() .
.
(2)解法一、因为M,N是y轴上不同的两点,两点的纵坐标互为倒数,
设M,N坐标为(0,m),(0,n),则![]() ,m≠0,n≠0
,m≠0,n≠0
由A(2,0),M(0,m)得直线AM的方程为![]() ,
,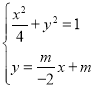 ,
,
整理得(m2+1)y2﹣2my=0或(m2+1)x2﹣4m2x+4m2﹣4=0,
得交点P的纵坐标为![]() ,
,
同理交点Q的纵坐标为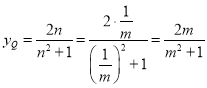 ,
,
所以yP=yQ≠0,直线PQ与x轴平行.
解法二:
设直线AM的方程为x=ty+2(t≠0),直线AN的方程为x=sy+2(s≠0),
令x=0得tyM=﹣2,M坐标为![]() ,同理N坐标为
,同理N坐标为![]() ,
,
因为M,N是y轴上不同的两点,两点的纵坐标互为倒数,所以st=4,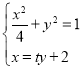 ,
,
整理得(t2+4)y2+4ty=0或(t2+4)x2﹣16x+16﹣4t2=0,
得交点P的纵坐标为![]() ,
,
同理得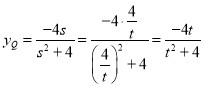 ,
,
所以yP=yQ≠0,直线PQ与x轴平行.
解法三:
设直线AM的方程为y=k1(x﹣2),k1≠0,直线AN的方程为y=k2(x﹣2),k2≠0
令x=0得M坐标为(0,﹣2k1),同理N坐标为(0,﹣2k2),
因为M,N是y轴上不同的两点,两点的纵坐标互为倒数,所以4k1k2=1,
代入椭圆方程得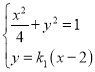 ,
,![]() ,
,
或![]() 所以
所以![]() ,
,
得交点P的纵坐标为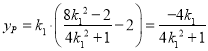 ,
,
同理得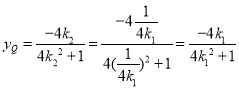 ,
,
所以yP=yQ≠0,直线PQ与x轴平行.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】数学中有许多寓意美好的曲线,曲线![]() 被称为“四叶玫瑰线”(如图所示).
被称为“四叶玫瑰线”(如图所示).

给出下列三个结论:
①曲线![]() 关于直线
关于直线![]() 对称;
对称;
②曲线![]() 上任意一点到原点的距离都不超过
上任意一点到原点的距离都不超过![]() ;
;
③存在一个以原点为中心、边长为![]() 的正方形,使得曲线
的正方形,使得曲线![]() 在此正方形区域内(含边界).
在此正方形区域内(含边界).
其中,正确结论的序号是________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】新中国成立70周年以来,党中央、国务院高度重视改善人民生活,始终把脱贫致富和提高人民生活水平作为一切工作的出发点和落脚点新疆某地区为了带动当地经济发展,大力发展旅游业,如图是2015—2019年到该地区旅游的游客数量(单位:万人次)的变化情况,则下列结论错误的是( )
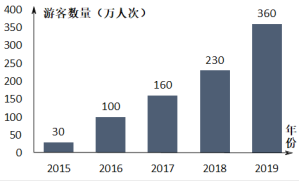
A.2015—2019年到该地区旅游的人数与年份成正相关
B.2019年到该地区旅游的人数是2015年的12倍
C.2016—2019年到该地区旅游的人数平均值超过了220万人次
D.从2016年开始,与上一年相比,2019年到该地区旅游的人数增加得最多
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在四棱锥![]() 中,底面
中,底面![]() 是正方形,顶点
是正方形,顶点![]() 在底面的射影是底面的中心,且各顶点都在同一球面上,若该四棱锥的侧棱长为
在底面的射影是底面的中心,且各顶点都在同一球面上,若该四棱锥的侧棱长为![]() ,体积为4,且四棱锥的高为整数,则此球的半径等于( )(参考公式:
,体积为4,且四棱锥的高为整数,则此球的半径等于( )(参考公式:![]() )
)
A. 2B. ![]() C. 4D.
C. 4D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】党的十八大以来,脱贫工作取得巨大成效,全国农村贫困人口大幅减少.如图的统计图反映了2012﹣2019年我国农村贫困人口和农村贫困发生率的变化情况(注:贫困发生率=贫困人数(人)÷统计人数(人)×100%).根据统计图提供的信息,下列推断不正确的是( )
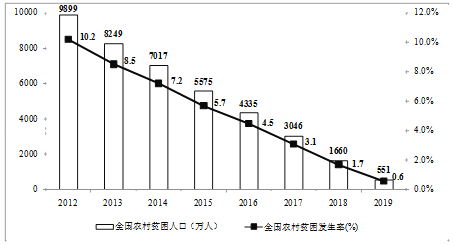
A.2012﹣2019年,全国农村贫困人口逐年递减
B.2013﹣2019年,全国农村贫困发生率较上年下降最多的是2013年
C.2012﹣2019年,全国农村贫困人口数累计减少9348万
D.2019年,全国各省份的农村贫困发生率都不可能超过0.6%
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,曲线E的参数方程为![]() (
(![]() 为参数),以O为极点,x轴非负半轴为极轴建立极坐标系,直线
为参数),以O为极点,x轴非负半轴为极轴建立极坐标系,直线![]() ,
,![]() 的极坐标方程分别为
的极坐标方程分别为![]() ,
,![]() ,
,![]() 交曲线E于点A,B,
交曲线E于点A,B,![]() 交曲线E于点C,D.
交曲线E于点C,D.
(1)求曲线E的普通方程及极坐标方程;
(2)求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com