
���� ��1���Ĵ�ʵ�����ʱ��ʵ��ɹ��Ĵ�������Ϊ0��1��2��3��4��ʵ��ʧ�ܵĴ�������Ϊ4��3��2��1��0���εĿ���ȡֵΪ4��2��0���ֱ������Ӧ�ĸ��ʣ��ɴ�������εķֲ��к�������
��2���εĿ���ȡֵΪ0��2��4������=0ʱ������ʽΪ1��0��x��R��������⼯ΪR������=2ʱ������ʽΪ2x2-2x+1��0���⼯ΪR����=4ʱ������ʽΪ4x2-4x+1��0���⼯Ϊ$\left\{{x\left|{x=\frac{1}{2}}\right.}\right\}$����ΪR���ɴ�������¼�A�����ĸ���P��A����
��� �⣺��1���Ĵ�ʵ�����ʱ��ʵ��ɹ��Ĵ�������Ϊ0��1��2��3��4��
��Ӧ�أ�ʵ��ʧ�ܵĴ�������Ϊ4��3��2��1��0��
���ԦεĿ���ȡֵΪ4��2��0��
$P��{��=4}��=C_4^4{��{\frac{1}{3}}��^4}{��{\frac{2}{3}}��^0}+C_4^0{��{\frac{1}{3}}��^0}{��{\frac{2}{3}}��^4}=\frac{17}{81}$��
$P��{��=2}��=C_4^3{��{\frac{1}{3}}��^3}��{\frac{2}{3}}��+C_4^1��{\frac{1}{3}}��{��{\frac{2}{3}}��^3}=\frac{40}{81}$��
$P��{��=0}��=C_4^2{��{\frac{1}{3}}��^2}{��{\frac{2}{3}}��^2}=\frac{24}{81}=\frac{8}{27}$��
���Ԧεķֱ���Ϊ��
| �� | 0 | 2 | 4 |
| P | $\frac{8}{27}$ | $\frac{40}{81}$ | $\frac{17}{81}$ |
���� ���⿼����ʵ���������ɢ������¼��ķֲ��к���ѧ�����������е��⣬����ʱҪ�������⣬ע��ȿ����¼����ʼ��㹫ʽ�ĺ������ã�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��֪A��Բ�Ķ��㣬BD��Բ�����ֱ����C�ǵ���Բ����һ�㣬BD=2��BC=1��AC��������ɽǵĴ�СΪ$\frac{��}{3}$������A������ABC��ACD����ȥ���ֺ�ļ�������ͼ��ʾ��
��֪A��Բ�Ķ��㣬BD��Բ�����ֱ����C�ǵ���Բ����һ�㣬BD=2��BC=1��AC��������ɽǵĴ�СΪ$\frac{��}{3}$������A������ABC��ACD����ȥ���ֺ�ļ�������ͼ��ʾ���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
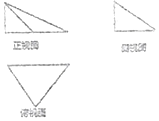 һ�������������ͼ��ͼ��ʾ�����и���ͼ��һ������Ϊ2�ĵ���ֱ�������Σ�����ͼ��һ��ֱ�DZ߳�Ϊ1��ֱ�������Σ���ü���������������ǣ�������
һ�������������ͼ��ͼ��ʾ�����и���ͼ��һ������Ϊ2�ĵ���ֱ�������Σ�����ͼ��һ��ֱ�DZ߳�Ϊ1��ֱ�������Σ���ü���������������ǣ�������| A�� | 36�� | B�� | 9�� | C�� | $\frac{9}{2}��$ | D�� | $\frac{27}{5}��$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\sqrt{3}+1$ | B�� | $\sqrt{3}-1$ | C�� | 4 | D�� | 2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\sqrt{3}$ | B�� | $\sqrt{2}$ | C�� | 2 | D�� | 3 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
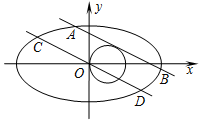 ��֪��ԲC1��$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1��a��b��0����������e=$\frac{{\sqrt{3}}}{2}$���ҹ���$��{2��\sqrt{3}}����$��ֱ��l1��y=kx+m��m��0����ԲC2����x-1��2+y2=1����������ԲC1����A��B���㣮
��֪��ԲC1��$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1��a��b��0����������e=$\frac{{\sqrt{3}}}{2}$���ҹ���$��{2��\sqrt{3}}����$��ֱ��l1��y=kx+m��m��0����ԲC2����x-1��2+y2=1����������ԲC1����A��B���㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $��\frac{7��}{12}��0��$ | B�� | $��\frac{��}{6}��0��$ | C�� | $��\frac{5��}{8}��0��$ | D�� | $��\frac{2��}{3}��-3��$ |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com