
【题目】如图,四边形![]() 为正方形,
为正方形,![]() 分别为
分别为![]() 的中点,以
的中点,以![]() 为折痕把
为折痕把![]() 折起,使点
折起,使点![]() 到达点
到达点![]() 的位置,且
的位置,且![]() .
.
(1)证明:平面![]() 平面
平面![]() ;
;
(2)求![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.

【答案】(1)证明见解析.
(2) ![]() .
.
【解析】分析:(1)首先从题的条件中确定相应的垂直关系,即BF⊥PF,BF⊥EF,又因为![]() ,利用线面垂直的判定定理可以得出BF⊥平面PEF,又
,利用线面垂直的判定定理可以得出BF⊥平面PEF,又![]() 平面ABFD,利用面面垂直的判定定理证得平面PEF⊥平面ABFD.
平面ABFD,利用面面垂直的判定定理证得平面PEF⊥平面ABFD.
(2)结合题意,建立相应的空间直角坐标系,正确写出相应的点的坐标,求得平面ABFD的法向量,设DP与平面ABFD所成角为![]() ,利用线面角的定义,可以求得
,利用线面角的定义,可以求得 ,得到结果.
,得到结果.
详解:(1)由已知可得,BF⊥PF,BF⊥EF,又![]() ,所以BF⊥平面PEF.
,所以BF⊥平面PEF.
又![]() 平面ABFD,所以平面PEF⊥平面ABFD.
平面ABFD,所以平面PEF⊥平面ABFD.
(2)作PH⊥EF,垂足为H.由(1)得,PH⊥平面ABFD.
以H为坐标原点,![]() 的方向为y轴正方向,
的方向为y轴正方向,![]() 为单位长,建立如图所示的空间直角坐标系Hxyz.
为单位长,建立如图所示的空间直角坐标系Hxyz.
由(1)可得,DE⊥PE.又DP=2,DE=1,所以PE=![]() .又PF=1,EF=2,故PE⊥PF.
.又PF=1,EF=2,故PE⊥PF.
可得![]() .
.
则![]()
![]() 为平面ABFD的法向量.
为平面ABFD的法向量.
设DP与平面ABFD所成角为![]() ,则
,则 .
.
所以DP与平面ABFD所成角的正弦值为![]() .
.


 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:高中数学 来源: 题型:
【题目】已知圆M的方程为x2+y2-2x-2y-6=0,以坐标原点O为圆心的圆O与圆M相切.
(1)求圆O的方程;
(2)圆O与x轴交于E,F两点,圆O内的动点D使得DE,DO,DF成等比数列,求![]()
![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着我国经济实力的不断提升,居民收人也在不断增加。某家庭2018年全年的收入与2014年全年的收入相比增加了一倍,实现翻番.同时该家庭的消费结构随之也发生了变化,现统计了该家庭这两年不同品类的消费额占全年总收入的比例,得到了如下折线图:
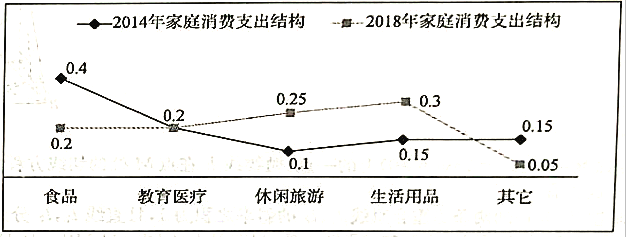
则下列结论中正确的是( )
A. 该家庭2018年食品的消费额是2014年食品的消费额的一半
B. 该家庭2018年教育医疗的消费额与2014年教育医疗的消费额相当
C. 该家庭2018年休闲旅游的消费额是2014年休闲旅游的消费额的五倍
D. 该家庭2018年生活用品的消费额是2014年生活用品的消费额的两倍
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图(1),等腰梯形![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分别是
分别是![]() 的两个三等分点,若把等腰梯形沿虚线
的两个三等分点,若把等腰梯形沿虚线![]() 、
、![]() 折起,使得点
折起,使得点![]() 和点
和点![]() 重合,记为点
重合,记为点![]() , 如图(2).
, 如图(2).

(1)求证:平面![]() 平面
平面![]() ;
;
(2)求平面![]() 与平面
与平面![]() 所成锐二面角的余弦值.
所成锐二面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() 是抛物线
是抛物线![]() 上一点,
上一点,![]() 为
为![]() 的焦点.
的焦点.
(1)若![]() ,
,![]() 是
是![]() 上的两点,证明:
上的两点,证明:![]() ,
,![]() ,
,![]() 依次成等比数列.
依次成等比数列.
(2)过![]() 作两条互相垂直的直线与
作两条互相垂直的直线与![]() 的另一个交点分别交于
的另一个交点分别交于![]() ,
,![]() (
(![]() 在
在![]() 的上方),求向量
的上方),求向量![]() 在
在![]() 轴正方向上的投影的取值范围.
轴正方向上的投影的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某城市交通部门为了对该城市共享单车加强监管,随机选取了100人就该城市共享单车的推行情况进行问卷调查,并将问卷中的这100人根据其满意度评分值(百分制)按照![]() 分成5组,制成如图所示频率分直方图.
分成5组,制成如图所示频率分直方图.

(1)求图中x的值;
(2)求这组数据的平均数和中位数;
(3)已知满意度评分值在![]() 内的男生数与女生数3:2,若在满意度评分值为
内的男生数与女生数3:2,若在满意度评分值为![]() 的人中随机抽取2人进行座谈,求2人均为男生的概率.
的人中随机抽取2人进行座谈,求2人均为男生的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com