
分析 设长方体的三度为,a,b,c,所求三棱锥的体积为:abc-4×$\frac{1}{3}×\frac{1}{2}abc$=$\frac{1}{3}$abc.底面三角形是等腰三角形时,m=n=$\sqrt{6}$时,能求出三棱锥体积的最大值.
解答 解:如图设长方体的三度为,a,b,c,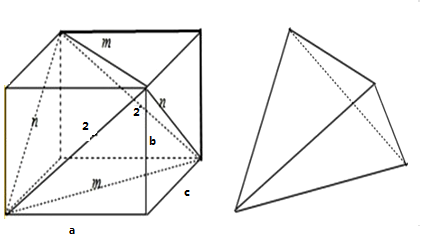
所求三棱锥的体积为:
abc-4×$\frac{1}{3}×\frac{1}{2}abc$=$\frac{1}{3}$abc.
a2+b2=4,b2+c2=n2,a2+c2=m2,
所以2(a2+b2+c2)
=n2+m2+4=16.
a2+b2+c2=8.
因为8≥$3\root{3}{(abc)^{2}}$,abc≤$\sqrt{(\frac{8}{3})^{3}}$=$\frac{16\sqrt{6}}{9}$,
此时a=b=c,与n2+m2=12,a2+b2=4,矛盾;
当底面三角形是等腰三角形时,m=n=$\sqrt{6}$,
三棱锥体积的最大值为:$\frac{4}{3}$.
故答案为:$\frac{4}{3}$.
点评 本题考查几何体的体积的求法,扩展为长方体是解题的关键,考查基本不等式的应用,转化思想与计算能力.


 天天练口算系列答案
天天练口算系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
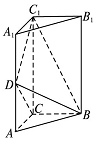 如图,直三棱柱(侧棱垂直于底面)ABC-A1B1C1中,$CA=CB=\frac{1}{2}C{C_1}$,点D棱AA1的中点,且C1D⊥BD.
如图,直三棱柱(侧棱垂直于底面)ABC-A1B1C1中,$CA=CB=\frac{1}{2}C{C_1}$,点D棱AA1的中点,且C1D⊥BD.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{2π}{3}$ | D. | $\frac{5π}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充要条件 | B. | 必要不充分 | ||
| C. | 充分不必要 | D. | 既不充分也不必要 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 空间四边形 | B. | 任意的四边形 | C. | 梯形 | D. | 平行四边形 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
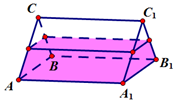 如图,一个直三棱柱形容器中盛有水,且侧棱AA1=8.若侧面AA1B1B水平放置时,液面恰好过AC,BC,A1C1,B1C1的中点,当底面ABC水平放置时,液面高为( )
如图,一个直三棱柱形容器中盛有水,且侧棱AA1=8.若侧面AA1B1B水平放置时,液面恰好过AC,BC,A1C1,B1C1的中点,当底面ABC水平放置时,液面高为( )| A. | 7 | B. | 6 | C. | 4 | D. | 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com