
【题目】已知函数![]() ,函数
,函数![]() 与直线
与直线![]() 相切,其中
相切,其中![]() ,
,![]() ,
,![]() 是自然对数的底数.
是自然对数的底数.
(1)求实数![]() 的值;
的值;
(2)设函数![]() 在区间
在区间![]() 内有两个极值点.
内有两个极值点.
①求![]() 的取值范围;
的取值范围;
②设函数![]() 的极大值和极小值的差为
的极大值和极小值的差为![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案科目:高中数学 来源: 题型:
【题目】某人某天的工作是驾车从![]() 地出发,到
地出发,到![]() 两地办事,最后返回
两地办事,最后返回![]() 地,
地,![]() ,三地之间各路段行驶时间及拥堵概率如下表
,三地之间各路段行驶时间及拥堵概率如下表
路段 | 正常行驶所用时间(小时) | 上午拥堵概率 | 下午拥堵概率 |
| 1 | 0.3 | 0.6 |
| 2 | 0.2 | 0.7 |
| 3 | 0.3 | 0.9 |
若在某路段遇到拥堵,则在该路段行驶时间需要延长1小时.
现有如下两个方案:
方案甲:上午从![]() 地出发到
地出发到![]() 地办事然后到达
地办事然后到达![]() 地,下午从
地,下午从![]() 地办事后返回
地办事后返回![]() 地;
地;
方案乙:上午从![]() 地出发到
地出发到![]()
![]() 地出发到达
地出发到达![]() 地,办完事后返回
地,办完事后返回![]() 地.
地.
(1)若此人早上8点从![]() 地出发,在各地办事及午餐的累积时间为2小时,且采用方案甲,求他当日18点或18点之前能返回
地出发,在各地办事及午餐的累积时间为2小时,且采用方案甲,求他当日18点或18点之前能返回![]() 地的概率.
地的概率.
(2)甲乙两个方案中,哪个方案有利于办完事后更早返回![]() 地?请说明理由.
地?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,某市管辖的海域内有一圆形离岸小岛,半径为1公里,小岛中心O到岸边AM的最近距离OA为2公里.该市规划开发小岛为旅游景区,拟在圆形小岛区域边界上某点B处新建一个浴场,在海岸上某点C处新建一家五星级酒店,在A处新建一个码头,且使得AB与AC满足垂直且相等,为方便游客,再建一条跨海高速通道OC连接酒店和小岛,设![]() .
.
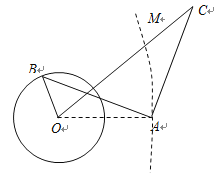
(1)设![]() ,试将
,试将![]() 表示成
表示成![]() 的函数;
的函数;
(2)若OC越长,景区的辐射功能越强,问当![]() 为何值时OC最长,并求出该最大值.
为何值时OC最长,并求出该最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在底面为直角梯形的四棱锥P-ABCD中,AD∥BC,∠ABC=90°,PA⊥平面ABCD,PA=3,AD=2,AB=2![]() ,BC=6.
,BC=6.
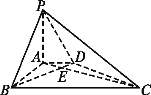
(1)求证:BD⊥平面PAC; (2)求二面角P-BD-A的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某大型商场的空调在1月到5月的销售量与月份相关,得到的统计数据如下表:
月份 | 1 | 2 | 3 | 4 | 5 |
销量 | 0.6 | 0.8 | 1.2 | 1.6 | 1.8 |
(1)经分析发现1月到5月的销售量可用线性回归模型拟合该商场空调的月销量![]() (百件)与月份
(百件)与月份![]() 之间的相关关系.请用最小二乘法求
之间的相关关系.请用最小二乘法求![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ,并预测6月份该商场空调的销售量;
,并预测6月份该商场空调的销售量;
(2)若该商场的营销部对空调进行新一轮促销,对7月到12月有购买空调意愿的顾客进行问卷调查.假设该地拟购买空调的消费群体十分庞大,经过营销部调研机构对其中的500名顾客进行了一个抽样调查,得到如下一份频数表:
有购买意愿对应的月份 | 7 | 8 | 9 | 10 | 11 | 12 |
频数 | 60 | 80 | 120 | 130 | 80 | 30 |
现采用分层抽样的方法从购买意愿的月份在7月与12月的这90名顾客中随机抽取6名,再从这6人中随机抽取3人进行跟踪调查,求抽出的3人中恰好有2人是购买意愿的月份是12月的概率.
参考公式与数据:线性回归方程![]() ,其中
,其中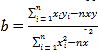 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,以
为极点,以![]() 轴正半轴为极轴,建立极坐标系,曲线
轴正半轴为极轴,建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的极坐标方程;
的极坐标方程;
(2)射线![]() 与曲线
与曲线![]() 分别交于
分别交于![]() 两点(异于原点
两点(异于原点![]() ),定点
),定点![]() ,求
,求![]() 的面积.
的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近年来,随着国家综合国力的提升和科技的进步,截至2018年底,中国铁路运营里程达13,2万千米,这个数字比1949年增长了5倍;高铁运营里程突破2.9万千米,占世界高铁运营里程的60%以上,居世界第一位下表截取了2012--2016年中国高铁密度的发展情况(单位:千米/万平方千米).
年份 | 2012 | 2013 | 2014 | 2015 | 2016 |
年份代码 | 1 | 2 | 3 | 4 | 5 |
高铁密度 | 9.75 | 11.49 | 17.14 | 20.66 | 22.92 |
已知高铁密度y与年份代码x之间满足关系式![]() (
(![]() 为大于0的常数)若对
为大于0的常数)若对![]() 两边取自然对数,得到
两边取自然对数,得到![]() ,可以发现
,可以发现![]() 与
与![]() 线性相关.
线性相关.
(1)根据所给数据,求y关于x的回归方程(![]() 保留到小数点后一位);
保留到小数点后一位);
(2)利用(1)的结论,预测到哪一年高铁密度会超过30千米/平方千米.
参考公式设具有线性相关系的两个变量![]() 的一组数据为
的一组数据为![]() ,
,
则回归方程![]() 的系数:
的系数: ,
,![]() .
.
参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】过抛物线C:x2=4y的准线上任意一点P作抛物线的切线PA,PB,切点分别为A,B,则A点到准线的距离与B点到准线的距离之和的最小值是( )
A.7B.6C.5D.4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com