
ЁОЬтФПЁПЮэіВЬьЦјЖдГЧЪаЛЗОГдьГЩКмДѓгАЯьЃЌАДееЙњМвЛЗБЃВПЗЂВМЕФБъзМЃКОгУёЧјЕФPM2.5ЃЈДѓЦјжажБОЖаЁгкЛђЕШгк2.5ЮЂУзЕФПХСЃЮяЃЉФъЦНОљХЈЖШВЛЕУГЌЙ§35ЮЂПЫ/СЂЗНУз.ФГЪаЛЗБЃВПУХМгЧПСЫЖдПеЦјжЪСПЕФМрВтЃЌГщШЁФГОгУёЧјМрВтЕуЕФ20ЬьPM2.5ЕФ24аЁЪБЦНОљХЈЖШЕФМрВтЪ§ОнЃЌжЦГЩОЅвЖЭМЃЌШчЭМЃК
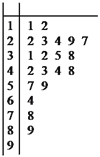
ЃЈЂёЃЉЭъГЩШчЯТЦЕТЪЗжВМБэЃЌВЂдкЫљИјЕФзјБъЯЕжаЛГі![]() ЕФЦЕТЪЗжВМжБЗНЭМЃЛ
ЕФЦЕТЪЗжВМжБЗНЭМЃЛ
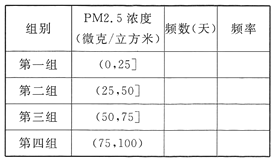
ЃЈЂђЃЉДгбљБОжаPM2.5ЕФ24аЁЪБЦНОљХЈЖШГЌЙ§50ЮЂПЫ/СЂЗНУзЕФЬьЪ§жаЃЌЫцЛњГщШЁ2ЬьЃЌЧѓЧЁКУгавЛЬьPM2.5ЕФ24аЁЪБЦНОљХЈЖШГЌЙ§75ЮЂПЫ/СЂЗНУзЕФИХТЪ.
ЁОД№АИЁПЃЈЂёЃЉМћНтЮіЃЈЂђЃЉ![]()
ЁОНтЮіЁПЪдЬтЗжЮіЃКЃЈЂёЃЉЭГМЦОЅвЖЭМЪ§ОнЃЌЧѓЕУИїзщЦЕЪ§КЭЦЕТЪЃЌВЂзїГіЗжЦЕБэЦЕТЪЗжВМжБЗНЭМЃЛ ЃЈЂђЃЉЯШЧѓЕУ![]() ЬьШЮШЁ
ЬьШЮШЁ![]() ЬьЃЌАќКЌЕФЛљБОЪТМўга
ЬьЃЌАќКЌЕФЛљБОЪТМўга![]() ИіЛљБОЪТМўЃЌЗћКЯЬѕМўЕФЙВ
ИіЛљБОЪТМўЃЌЗћКЯЬѕМўЕФЙВ![]() ИіЛљБОЪТМў
ИіЛљБОЪТМў![]() ЫљЧѓИХТЪЮЊЃК
ЫљЧѓИХТЪЮЊЃК![]() .
.
ЪдЬтНтЮіЃКЃЈЂёЃЉЦЕТЪЗжЦЕБэЦЕТЪЗжВМжБЗНЭМШчЯТЭМЫљЪОЃК

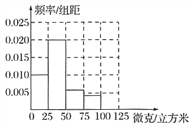
ЃЈЂђЃЉЩшPM2.5ЕФ24аЁЪБЦНОљХЈЖШдк![]() ФкЕФШ§ЬьМЧЮЊ
ФкЕФШ§ЬьМЧЮЊ![]() ЃЌ
ЃЌ
PM2.5ЕФ34аЁЪБЦНОљХЈЖШдк![]() ФкЕФСНЬьМЧЮЊ
ФкЕФСНЬьМЧЮЊ![]() ЃЌ
ЃЌ
Ёр5ЬьШЮШЁ2ЬьЃЌАќКЌЕФЛљБОЪТМўгаЃК
![]() ЃЛ
ЃЛ![]() ЃЛ
ЃЛ![]() ЃЛ
ЃЛ![]() ЃЌЙВ10ИіЛљБОЪТМўЃЌ
ЃЌЙВ10ИіЛљБОЪТМўЃЌ
ЩшЪТМў![]() ЧЁКУгавЛЬьPM2.5ЕФ24аЁЪБЦНОљХЈЖШГЌЙ§75ЮЂПЫ/СЂЗНУзЃЌдђАќКЌЕФЛљБОЪТМўга
ЧЁКУгавЛЬьPM2.5ЕФ24аЁЪБЦНОљХЈЖШГЌЙ§75ЮЂПЫ/СЂЗНУзЃЌдђАќКЌЕФЛљБОЪТМўга
![]() ЃЛ
ЃЛ![]() ЃЛ
ЃЛ![]() ЃЛЙВ6ИіЛљБОЪТМўЃЌ
ЃЛЙВ6ИіЛљБОЪТМўЃЌ
Ёр![]() ЃЌЁрДг5ЬьжаЫцЛњГщШЁ2ЬьЃЌЧЁКУгавЛЬьГЌЙ§75ЮЂПЫ/СЂЗНУзЕФИХТЪ
ЃЌЁрДг5ЬьжаЫцЛњГщШЁ2ЬьЃЌЧЁКУгавЛЬьГЌЙ§75ЮЂПЫ/СЂЗНУзЕФИХТЪ![]() .
.



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЫФРтзЖPЉABCDжаЃЌЦНУцPADЁЭЦНУцABCDЃЌAB=ADЃЌЁЯBAD=60ЁуЃЌEЁЂFЗжБ№ЪЧAPЁЂADЕФжаЕуЃЌЧѓжЄЃК 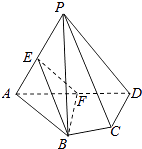
ЃЈ1ЃЉжБЯпEFЁЮЦНУцPCDЃЛ
ЃЈ2ЃЉЦНУцBEFЁЭЦНУцPADЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЯТСаУќЬтжаЃЌецУќЬтЪЧЃЈЁЁЁЁЃЉ
A.?x0ЁЪRЃЌ![]()
B.?xЁЪRЃЌ![]()
C.ЁАaЃО1ЃЌbЃО1ЁБЪЧЁАabЃО1ЁБЕФГфвЊЬѕМў
D.Щш![]() ЃЌ
ЃЌ ![]() ЮЊЯђСПЃЌдђЁА|
ЮЊЯђСПЃЌдђЁА|![]() ?
?![]() |=|
|=|![]() ||
||![]() |ЁБЪЧЁА
|ЁБЪЧЁА![]() ЁЮ
ЁЮ![]() ЁБЕФГфвЊЬѕМў
ЁБЕФГфвЊЬѕМў
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊКЏЪ§![]() ЃЈ
ЃЈ![]() ЃЉ.
ЃЉ.
ЃЈ1ЃЉШє![]() дкЕу
дкЕу![]() ДІЕФЧаЯпгыжБЯп
ДІЕФЧаЯпгыжБЯп![]() ДЙжБЃЌЧѓЪЕЪ§
ДЙжБЃЌЧѓЪЕЪ§![]() ЕФжЕЃЛ
ЕФжЕЃЛ
ЃЈ2ЃЉЧѓКЏЪ§![]() ЕФЕЅЕїЧјМфЃЛ
ЕФЕЅЕїЧјМфЃЛ
ЃЈ3ЃЉЬжТлКЏЪ§![]() дкЧјМф
дкЧјМф![]() ЩЯСуЕуЕФИіЪ§.
ЩЯСуЕуЕФИіЪ§.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЛЏМђЧѓжЕЃК
ЃЈ1ЃЉsinЃЈЉ1320ЁуЃЉcos1110Ёу+cosЃЈЉ1020ЁуЃЉsin750Ёу
ЃЈ2ЃЉ![]() ЃЎ
ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкБпГЄЮЊ2ЕФе§ЗНЬхABCDЉA1B1C1D1жаЃЌEЪЧBCЕФжаЕуЃЌFЪЧDD1ЕФжаЕуЃЌ
ЃЈ1ЃЉЧѓЕуAЕНЦНУцA1DEЕФОрРыЃЛ
ЃЈ2ЃЉЧѓжЄЃКCFЁЮЦНУцA1DEЃЛ
ЃЈ3ЃЉЧѓЖўУцНЧEЉA1DЉAЕФЦНУцНЧДѓаЁЕФгрЯвжЕЃЎ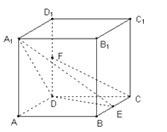
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкЁїABCжаЃЌШє ![]() =
= ![]() ЃЌдђЁїABCЕФаЮзДЪЧЃЈ ЃЉ
ЃЌдђЁїABCЕФаЮзДЪЧЃЈ ЃЉ
A.ШёНЧШ§НЧаЮ
B.жБНЧШ§НЧаЮ
C.ЕШбќШ§НЧаЮ
D.ЕШбќЛђжБНЧШ§НЧаЮ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЁїABCжаЃЌНЧAЃЌBЃЌCЕФЖдБпЗжБ№ЮЊaЃЌbЃЌcЃЌЧвcosC= ![]() ЃЎ
ЃЎ
ЃЈ1ЃЉЧѓНЧBЕФДѓаЁЃЛ
ЃЈ2ЃЉШєBDЮЊACБпЩЯЕФжаЯпЃЌcosA= ![]() ЃЌBD=
ЃЌBD= ![]() ЃЌЧѓЁїABCЕФУцЛ§ЃЎ
ЃЌЧѓЁїABCЕФУцЛ§ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊfЃЈxЃЉ= ![]() ЃЌgЃЈxЃЉ=
ЃЌgЃЈxЃЉ= ![]() ЃЎ
ЃЎ
ЃЈ1ЃЉЕБ1ЁмxЃМ2ЪБЃЌЧѓgЃЈxЃЉЃЛ
ЃЈ2ЃЉЕБxЁЪRЪБЃЌЧѓgЃЈxЃЉЕФНтЮіЪНЃЌВЂЛГіЦфЭМЯѓЃЛ 
ЃЈ3ЃЉЧѓЗНГЬxf[gЃЈxЃЉ]=2g[fЃЈxЃЉ]ЕФНтЃЎ
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com