
【题目】已知圆x2+y2+x-6y+m=0与直线x+2y-3=0相交于P、Q两点,O为原点,且OP⊥OQ,求实数m的值.
【答案】解:设点P、Q的坐标分别为(x1 , y1)、(x2 , y2).
由OP⊥OQ,得kOPkOQ=-1,即 ![]() .①
.①
联立 ![]() 得5x2+10x+4m-27=0,②
得5x2+10x+4m-27=0,②
∴x1+x2=-2,x1x2= ![]() . ③
. ③
∵P、Q是在直线x+2y-3=0上,
∴y1y2= ![]() (3-x1)·
(3-x1)· ![]() (3-x2)=
(3-x2)= ![]() [9-3(x1+x2)+x1x2].
[9-3(x1+x2)+x1x2].
将③代入,得y1y2= ![]() . ④
. ④
将③④代入①,解得m=3.代入方程②,检验Δ>0成立,
∴m=3
【解析】将直线和圆进行联立,利用根与系数之间的关系建立条件方程,利用韦达定理和两向量垂直的性质可以求出m的值来。
【考点精析】掌握数量积判断两个平面向量的垂直关系是解答本题的根本,需要知道若平面![]() 的法向量为
的法向量为![]() ,平面
,平面![]() 的法向量为
的法向量为![]() ,要证
,要证![]() ,只需证
,只需证![]() ,即证
,即证![]() ;即:两平面垂直
;即:两平面垂直![]() 两平面的法向量垂直.
两平面的法向量垂直.


 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案科目:高中数学 来源: 题型:
【题目】函数f(x)=-x3-2x2+4x,当x∈[-3,3]时,f(x)≥a有恒成立,则实数a的取值范围是( )
A.(-3,11)
B.[-33,+∞)
C.(-∞,-33]
D.[2,7]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《聊斋志异》中有这样一首诗:“挑水砍柴不堪苦,请归但求穿墙术.得诀自诩无所阻,额上坟起终不悟.”在这里,我们称形如以下形式的等式具有“穿墙术”: 2 ![]() =
= ![]() ,3
,3 ![]() =
= ![]() ,4
,4 ![]() =
= ![]() ,5
,5 ![]() =
= ![]()
则按照以上规律,若8 ![]() =
= ![]() 具有“穿墙术”,则n=( )
具有“穿墙术”,则n=( )
A.7
B.35
C.48
D.63
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】太极图是由黑白两个鱼形纹组成的图案,俗称阴阳鱼,太极图展现了一种相互转化,相互统一的和谐美.定义:能够将圆O的周长和面积同时等分成两部分的函数称为圆煌一个“太极函数”下列有关说法中: 
①对圆O:x2+y2=1的所有非常数函数的太极函数中,一定不能为偶函数;
②函数f(x)=sinx+1是圆O:x2+(y﹣1)2=1的一个太极函数;
③存在圆O,使得f(x)= ![]() 是圆O的太极函数;
是圆O的太极函数;
④直线(m+1)x﹣(2m+1)y﹣1=0所对应的函数一定是圆O:(x﹣2)2+(y﹣1)2=R2(R>0)的太极函数.
所有正确说法的序号是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆 ![]() : x2+y2+Dx+Ey+3=0 ,圆
: x2+y2+Dx+Ey+3=0 ,圆 ![]() 关于直线 x+y-1=0对称,圆心在第二象限,半径为
关于直线 x+y-1=0对称,圆心在第二象限,半径为![]() .
.
(1)求圆 ![]() 的方程;
的方程;
(2)已知不过原点的直线 l 与圆 ![]() 相切,且在
相切,且在 ![]() 轴、
轴、 ![]() 轴上的截距相等,求直线 l 的方程.
轴上的截距相等,求直线 l 的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲和乙参加有奖竞猜闯关活动,活动规则:①闯关过程中,若闯关成功则继续答题;若没通关则被淘汰;②每人最多闯3关;③闯第一关得10万奖金,闯第二关得20万奖金,闯第三关得30万奖金,一关都没过则没有奖金.已知甲每次闯关成功的概率为 ![]() ,乙每次闯关成功的概率为
,乙每次闯关成功的概率为 ![]() .
.
(1)设乙的奖金为ξ,求ξ的分布列和数学期望;
(2)求甲恰好比乙多30万元奖金的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知二次函数f(x)=ax2+bx(a,b为常数,且a≠0)满足条件:f(x﹣1)=f(3﹣x)且方程f(x)=2x有两个相等实数根 (Ⅰ)求f(x)的解析式;
(Ⅱ)是否存在实数m,n(m<n),使f(x)的定义域和值域分别为[m,n]和[4m,4n],如果存在,求出符合条件的所有m,n的值,如果不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标平面内,以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系,曲线C的极坐标方程是ρ=4sinθ,直线l的参数方程是 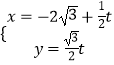 (t为参数).
(t为参数).
(1)求直线l的普通方程和曲线C的直角坐标方程;
(2)求曲线C上的点到直线l的距离的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com