
分析 (Ⅰ)利用任意角的三角函数的定义,求得sinα,cosα,tanα的值.
(Ⅱ)先求得 tan(α+β)的值,再根据α+β∈(0,π),求得α+β的值.
解答 解:(Ⅰ)∵锐角α,β的顶点与原点O重合,始边与x轴非负半轴重合,角α的终边经过点A(2,1),∴x=2,y=1,r=|OA|=$\sqrt{5}$,
∴sinα=$\frac{y}{r}$=$\frac{1}{\sqrt{5}}$=$\frac{\sqrt{5}}{5}$,cosα=$\frac{x}{r}$=$\frac{2}{\sqrt{5}}$=$\frac{2\sqrt{5}}{5}$,tanα=$\frac{y}{x}$=$\frac{1}{2}$.
(Ⅱ)∵角β的终边经过点B(3,1),∴tanβ=$\frac{1}{3}$.
又 tan(α+β)=$\frac{tanα+tanβ}{1-tanα•tanβ}$=1,α+β∈(0,π),∴α+β=$\frac{π}{4}$,
点评 本题主要考查任意角的三角函数的定义,两角和的正切公式,根据三角函数值求角,属于基础题.


 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案科目:高中数学 来源: 题型:解答题
 长方体截去一个三棱锥后的直观图和部分三视图如图所示.
长方体截去一个三棱锥后的直观图和部分三视图如图所示.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
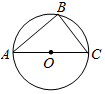 如图所示,圆O的半径为R,A、B、C为圆O上不同的三点,圆心O在线段AC上.
如图所示,圆O的半径为R,A、B、C为圆O上不同的三点,圆心O在线段AC上.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{6}$ | B. | $\frac{1}{4}$ | C. | $\frac{3}{4}$ | D. | $\frac{5}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,+∞) | B. | (-∞,1) | C. | (-∞,1] | D. | [1,+∞) |
查看答案和解析>>
科目:高中数学 来源:2016-2017学年内蒙古高二理上月考一数学理试卷(解析版) 题型:解答题
已知椭圆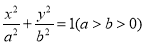 的左、右两个焦点
的左、右两个焦点 ,过其中两个端点的直线斜率为
,过其中两个端点的直线斜率为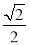 ,过两个焦点和一个顶点的三角形面积为1。
,过两个焦点和一个顶点的三角形面积为1。
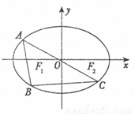
(1)求椭圆的方程;
(2)如图,点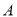 为椭圆上一动点(非长轴端点),
为椭圆上一动点(非长轴端点),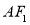 的延长线与椭圆交于
的延长线与椭圆交于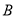 点,
点,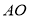 的延长线与椭圆交
的延长线与椭圆交
于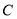 点,求
点,求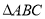 面积的最大值,并求此时直线
面积的最大值,并求此时直线 的方程,
的方程,
查看答案和解析>>
科目:高中数学 来源:2016-2017学年江西吉安一中高二上段考一数学(文)试卷(解析版) 题型:选择题
下列四个命题中错误的个数是( )
①垂直于同一条直线的两条直线相互平行;
②垂直于同一个平面的两条直线相互平行;
③垂直于同一条直线的两个平面相互平行;
④垂直于同一个平面的两个平面相互平行.
A.1 B.2 C.3 D. 4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com