
 ,-1),问是否存在经过A,B两点且与l1,l2都相切的圆,若存在,求出该圆的方程;若不存在,清说明理由。
,-1),问是否存在经过A,B两点且与l1,l2都相切的圆,若存在,求出该圆的方程;若不存在,清说明理由。 (Ⅰ)解:设点A,B的坐标分别为(x1,y1),(x2,y2),
l1,l2分别是抛物线C在点A,B处的切线,
∴直线l1的斜率为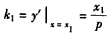 ,直线l2的斜率为
,直线l2的斜率为 ,
,
∵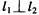 ,
,
∴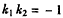 ,得
,得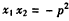 , ①
, ①
∵A,B是抛物线C上的点,
∴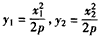 ,
,
∴直线l1的方程为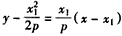 ,直线l2的方程为
,直线l2的方程为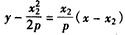 ,
,
由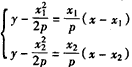 ,解得:
,解得: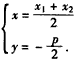 ,
,
∴点D的纵坐标为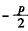 。
。
(Ⅱ)证法一:∵F为抛物线C的焦点,
∴ ,
,
∴直线AF的斜率为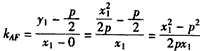 ,
,
直线BF的斜率为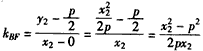 ,
,
∵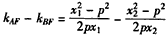

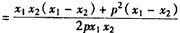
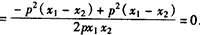 ,
,
∴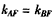 ,∴A,B,F三点共线。
,∴A,B,F三点共线。
证法二:∵F为抛物线C的焦点,
∴ ,
,
∴ ,
,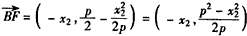 ,
,
∵ ,
,
∴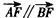 ,
,
∴A,B,F三点共线。
(Ⅲ)解:不存在,
证明如下:假设存在符合题意的圆,
设该圆的圆心为M,依题意,得MA⊥AD,MB⊥BD,且|MA|=|MB|,
由l1⊥l2,得AD⊥BD,
∴四边形MADB是正方形,∴|AD|=|BD|,
∵点D的坐标为(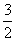 ,-1),∴
,-1),∴ ,即p=2,
,即p=2,
把点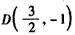 代入直线l1,得
代入直线l1,得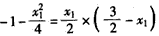 ,
,
解得: 或
或 ,
,
∴点A的坐标为(4,4)或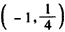 ,
,
同理可求得点B的坐标为(4,4)或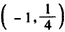 ,
,
由于A,B是抛物线C上的不同两点,
不妨令 ,
,
∴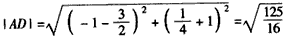 ,
,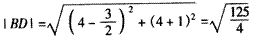 ,
,
∴|AD|≠|BD|,这与|AD|= |BD|矛盾,
∴经过A,B两点且与l1,l2都相切的圆不存在。


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
| 1 | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| 2 |
| AF |
| FB |
| AB |
| FQ |
查看答案和解析>>
科目:高中数学 来源: 题型:
| ||
|
|
|
| ||
|
|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com