练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    已知A(3．3，1)、B(1，0，5)，求：(1)线段|AB|的长度；(2)线段AB的中点坐标；(3)到A、B两点距离相等的点P(x，y，z)的坐标x、y、z满足的条件．

    答案：略
    解析：

    (1)由空间两点间的距离公式得

    ．

    (2)线段AB的中点坐标为，即为．

    (3)点P(x，y，z)到A、B的距离相等，则

    ，化简得4x+6y－8z+7=0．

    即到A、B距离相等的点的坐标(x，y，z)满足的条件是4x+6y－8z+7=0．


    提示：

    在空间直角坐标系中，已知A(，，)，B(，，)，则；线段AB的中点坐标是．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    已知|
    a
    |=3，|
    b
    |=1，且
    a
    与
    b
    同向共线，则
    a
    •
    b
    的值是（　　）
    A、-3B、0C、3D、-3或3

    查看答案和解析>>

    科目：高中数学 来源：走向清华北大同步导读·高二数学(上) 题型：013

    已知A(3，3)、B(－1，5)，直线l：y＝1－ax与线段AB有公共点，则a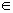

    [　　]

    A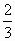．[－，4]　　　　　　　B．(－∞，)(，＋∞)

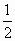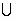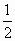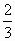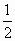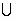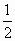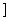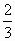
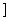
    C．[－，](，4　　D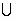．(－∞，－(4，＋∞)

    查看答案和解析>>

    科目：高中数学 来源：安徽省宿州市十三所重点中学2011－2012学年高二下学期期中质量检测数学文科试题 题型：013

    下列命题中正确的是

    (1)已知a，b∈R，则a＝b是(a－b)＋(a＋b)i为纯虚数的充要条件

    (2)当z是非零实数时，恒成立

    (3)复数z＝(1－i)3的实部和虚部都是－2

    (4)设z的共轭复数为，若

    [　　]

    A．(1)(2)

    B．(1)(3)

    C．(2)(3)

    D．(2)(4)

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知a>0，函数f(x)=ax－bx2,

    （1）当b>0时，若对任意x∈R都有f(x)≤1，证明：a≤2；

    （2）当b>1时，证明：对任意x∈[0, 1], |f(x)|≤1的充要条件是：b－1≤a≤2；

    （3）当0≤1时，讨论：对任意x∈[0, 1], |f(x)|≤1的充要条件。

     

    查看答案和解析>>

    同步练习册答案