
分析 (Ⅰ)由题意可知:RN=RM,即点R到直线x=-1和点M的距离相等,利用抛物线的定义求曲线E的方程;
(Ⅱ)联立$\left\{\begin{array}{l}y=kx+b\\{y^2}=4x\end{array}\right.$,消去y,证明kAP=kAQ,可得A,P,Q三点共线.
解答 (Ⅰ)解:由题意可知:RN=RM,即点R到直线x=-1和点M的距离相等.
根据抛物线的定义可知:R的轨迹为抛物线,其中M为焦点.
设R的轨迹方程为:y2=2px,$\frac{p}{2}=1$,p=2
所以R的轨迹方程为:y2=4x.…(5分)
(Ⅱ证明:由条件可知$C(-\frac{b}{k},0)$,则$Q(\frac{b}{k},0)$.
联立$\left\{\begin{array}{l}y=kx+b\\{y^2}=4x\end{array}\right.$,消去y得k2x2+(2bk-4)x+b2=0,△=(2bk-4)2-4b2k2=16(1-bk)>0.
设A(x1,y1),B(x2,y2)(x1<x2),则P(x2,-y2)
${x_1}+{x_2}=\frac{4-2bk}{k^2}$,${x_1}=\frac{{4-2bk-4\sqrt{1-bk}}}{{2{k^2}}}$,${x_2}=\frac{{4-2bk+4\sqrt{1-bk}}}{{2{k^2}}}$.
因为${k_{AP}}=\frac{{{y_1}+{y_2}}}{{{x_1}-{x_2}}}=\frac{{k({x_1}+{x_2})+2b}}{{\frac{{-8\sqrt{1-bk}}}{{2{k^2}}}}}=\frac{-k}{{\sqrt{1-bk}}}$,${k}_{AQ}=\frac{{y}_{1}-0}{{x}_{1}-\frac{b}{k}}=\frac{k(k{x}_{1}+b)}{k{x}_{1}-b}=\frac{2(1-\sqrt{1-bk})}{\frac{2[(1-bk)-\sqrt{1-bk}]}{2k}}=\frac{k}{-\sqrt{1-bk}}$
所以kAP=kAQ,
所以A,P,Q三点共线.…(13分)
点评 本题考查抛物线的定义,考查直线与抛物线的位置关系,考查韦达定理的运用,属于中档题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
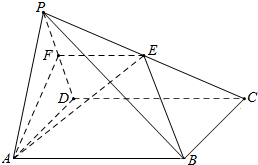 如图,在四棱锥P-ABCD中,底面ABCD是正方形.点E是棱PC的中点,平面ABE与棱PD交于点F.
如图,在四棱锥P-ABCD中,底面ABCD是正方形.点E是棱PC的中点,平面ABE与棱PD交于点F.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com