
【题目】已知函数![]() .
.
(1)当![]() 时,求
时,求![]() 的单调区间;
的单调区间;
(2)设![]() ,
, ![]() 是曲线
是曲线![]() 图象上的两个相异的点,若直线
图象上的两个相异的点,若直线![]() 的斜率
的斜率![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围;
的取值范围;
(3)设函数![]() 有两个极值点
有两个极值点![]() ,
, ![]() ,且
,且![]() ,若
,若![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知曲线
中,已知曲线![]() (θ为参数),将
(θ为参数),将![]() 上的所有点的横坐标、纵坐标分别伸长为原来的
上的所有点的横坐标、纵坐标分别伸长为原来的![]() 和2倍后得到曲线
和2倍后得到曲线![]() ,以平面直角坐标系
,以平面直角坐标系![]() 的原点
的原点![]() 为极点,
为极点, ![]() 轴的正半轴为极轴,取相同的单位长度建立极坐标系,已知直线
轴的正半轴为极轴,取相同的单位长度建立极坐标系,已知直线![]() .
.
(1)试写出曲线![]() 的极坐标方程与曲线
的极坐标方程与曲线![]() 的参数方程;
的参数方程;
(2)在曲线![]() 上求一点
上求一点![]() ,使点
,使点![]() 到直线
到直线![]() 的距离最小,并求此最小值.
的距离最小,并求此最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(A)在直角坐标系![]() 中,以坐标原点为极点,
中,以坐标原点为极点, ![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的参数方程为
的参数方程为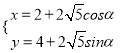 (
(![]() 为参数),
为参数), ![]() 是曲线
是曲线![]() 上的动点,
上的动点, ![]() 为线段
为线段![]() 的中点,设点
的中点,设点![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
(1)求![]() 的坐标方程;
的坐标方程;
(2)若射线![]() 与曲线
与曲线![]() 异于极点的交点为
异于极点的交点为![]() ,与曲线
,与曲线![]() 异于极点的交点为
异于极点的交点为![]() ,求
,求![]() .
.
(B)设函数![]() .
.
(1)当![]() 时,求不等式
时,求不等式![]() 的解集;
的解集;
(2)对任意![]() ,
, ![]() 不等式
不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分12分)已知函数![]() 是自然对数的底数,
是自然对数的底数, ![]() .
.
(1)求函数![]() 的单调递增区间;
的单调递增区间;
(2)若![]() 为整数,
为整数, ![]() ,且当
,且当![]() 时,
时, ![]() 恒成立,其中
恒成立,其中![]() 为
为![]() 的导函数,求
的导函数,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了调查某生产线上质量监督员甲对产品质量好坏有无影响,现统计数据如下:质量监督员甲在生产现场时,990件产品中合格品有982件,次品有8件;甲不在生产现场时,510件产品中合格品有493件,次品有17件,试分别用列联表、独立性检验的方法分析监督员甲是否在生产现场对产品质量好坏有无影响?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程.
已知曲线![]() 在直角坐标系
在直角坐标系![]() 下的参数方程为
下的参数方程为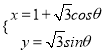 (
(![]() 为参数).以
为参数).以![]() 为极点,
为极点, ![]() 轴的非负半轴为极轴建立极坐标系.
轴的非负半轴为极轴建立极坐标系.
(1)求曲线![]() 的极坐标方程;
的极坐标方程;
(2)直线![]() 的极坐标方程是
的极坐标方程是![]() ,射线
,射线![]() 与曲线
与曲线![]() 交于
交于![]() 点,与直线
点,与直线![]() 交于
交于![]() ,求线段
,求线段![]() 的长.
的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业常年生产一种出口产品,根据预测可知,进入21世纪以来,该产品的产量平稳增长.记2009年为第1年,且前4年中,第x年与年产量f(x) 万件之间的关系如下表所示:
x | 1 | 2 | 3 | 4 |
f(x) | 4.00 | 5.58 | 7.00 | 8.44 |
若f(x)近似符合以下三种函数模型之一:f(x)=ax+b,f(x)=2x+a,f(x)=log![]() x+a.
x+a.
(1)找出你认为最适合的函数模型,并说明理由,然后选取其中你认为最适合的数据求出相应的解析式;
(2)因遭受某国对该产品进行反倾销的影响,2015年的年产量比预计减少30%,试根据所建立的函数模型,确定2015年的年产量.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com