练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

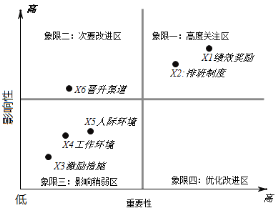
    【题目】2020年1月，某公司以问卷的形式调查影响员工积极性的六项关键指标：绩效奖励、排班制度、激励措施、工作环境、人际关系、晋升渠道，在确定各项指标权重结果后，进而得到指标重要性分析象限图（如图）.若客户服务中心从中任意抽取不同的两项进行分析，则这两项来自影响稍弱区的概率为（ ）

    A.B.C.D.

    【答案】A

    【解析】

    根据图可知，来自影响稍弱区的指标有激励措施、工作环境、人际关系三项，记为，其余三项记为，列举出从中任选两项的基本事件的总数，再找出两项来自影响稍弱区的基本事件的个数，代入古典概型的概率公式求解.

    由图可知，来自影响稍弱区的指标有激励措施、工作环境、人际关系三项，设为，其余三项设为，

    则从中任选两项的结果为，，，，，，，，，，，

    ，，，共种结果，

    这两项来自影响稍弱区的结果为，，共种，

    故概率.

    故选：A

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】为解决城市的拥堵问题，某城市准备对现有的一条穿城公路MON进行分流，已知穿城公路MON自西向东到达城市中心点O后转向东北方向（即）．现准备修建一条城市高架道路L，L在MO上设一出入口A，在ON上设一出入口B．假设高架道路L在AB部分为直线段，且要求市中心O与AB的距离为10km．

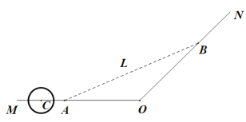
    （1）求两站点A，B之间距离的最小值；

    （2）公路MO段上距离市中心O30km处有一古建筑群C，为保护古建筑群，设立一个以C为圆心，5km为半径的圆形保护区．则如何在古建筑群C和市中心O之间设计出入口A，才能使高架道路L及其延伸段不经过保护区（不包括临界状态）？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数.

    （1）求函数的单调区间；

    （2）对a∈(0，1)，是否存在实数λ，，使成立，若存在，求λ的取值范围；若不存在，请说明理由.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知直线与椭圆交于不同的两点，线段的中点为，且直线与直线的斜率之积为.若直线与直线交于点，与直线交于点，且点为直线上一点.

    （1）求的轨迹方程；

    （2）若为椭圆的上顶点，直线与轴交点，记表示面积，求的最大值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在直角坐标系中，曲线的参数方程为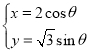（为参数），若以坐标原点O为极点，x轴正半轴为极轴建立极坐标系，曲线的极坐标方程为.

    （1）求曲线的普通方程和曲线的直角坐标方程；

    （2）若点P的坐标为，且曲线与曲线交于C，D两点，求的值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在平面直角坐标系中，已知曲线的参数方程：（为参数），以坐标原点为极点，以轴的正半轴为极轴建立极坐标系，曲线的极坐标方程为.

    （1）求曲线的普通方程；

    （2）过曲线上一点作直线与曲线交于两点，中点为，，求的最小值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】为了进一步激发同学们的学习热情，某班级建立了数学英语两个学习兴趣小组，两组的人数如下表所示：

    组别

    性别

    数学

    英语

    男

    5

    1

    女

    3

    3

    现采用分层抽样的方法(层内采用简单随机抽样)从两组中共抽取3名同学进行测试.

    （1）求从数学组抽取的同学中至少有1名女同学的概率；

    （2）记ξ为抽取的3名同学中男同学的人数，求随机变量ξ的分布列和数学期望.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】2020年春季，某出租汽车公同决定更换一批新的小汽车以代替原来报废的出租车，现有A，B两款车型，根据以这往这两种租车车型的数据，得到两款出租车型使用寿命频数表如表：

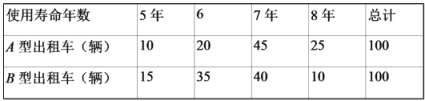
    （1）填写下表，并判断是否有99%的把握认为出租车的使用寿命年数与汽车车型有关？

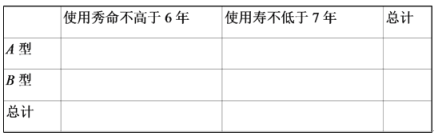
    （2）司机师傅小李准备在一辆开了4年的A型车和一辆开了4年的B型车中选择，为了尽最大可能实现3年内（含3年）不换车，试通过计算说明，他应如何选择.

    参考公式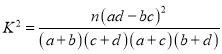：，其中n＝a+b+c+d.

    参考数据：

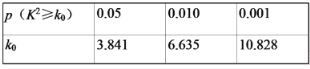
    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，四棱锥S﹣ABCD中，SD＝CD＝SC＝2AB＝2BC，平面ABCD⊥底面SDC，AB∥CD，∠ABC＝90°，E是SD中点．

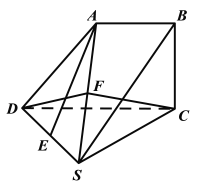
    （1）证明：直线AE//平面SBC；

    （2）点F为线段AS的中点，求二面角F﹣CD﹣S的大小．

    查看答案和解析>>

    同步练习册答案