
【题目】从3名男生和2名女生中任选两人参加演讲比赛,试求:
(1)所选2人都是男生的概率;
(2)所选2人恰有1名女生的概率;
(3)所选2人至少有1名女生的概率.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() 。
。
【解析】
试题分析:设3名男生编号为A1,A2,A3,两名女生的编号为B1,B2,那么从5人中任选两人,基本事件的为:(A1,A2),(A1,A3),(A1,B1),(A1,B2),(A2,A3),(A2,B1),(A2,B2),(A3,B1),(A3,B2),(B1,B2),共10种。(1)设事件A=“所选两人都是男生”,则A包含(A1,A2),(A1,A3),(A2,A3),共3个基本事件,所以![]() ;(2)设事件B“所选2人中恰有1名女生”,则B包含(A1,B1),(A1,B2),(A2,B1),(A2,B2),(A3,B1),(A3,B2),共6个基本事件,所以事件B的概率为
;(2)设事件B“所选2人中恰有1名女生”,则B包含(A1,B1),(A1,B2),(A2,B1),(A2,B2),(A3,B1),(A3,B2),共6个基本事件,所以事件B的概率为![]() ;(3)设事件C=“所选2人至少有1名女生”,则C包含(A1,B1),(A1,B2),(A2,B1),(A2,B2),(A3,B1),(A3,B2),(B1,B2),共7个基本事件,所以事件C的概率为
;(3)设事件C=“所选2人至少有1名女生”,则C包含(A1,B1),(A1,B2),(A2,B1),(A2,B2),(A3,B1),(A3,B2),(B1,B2),共7个基本事件,所以事件C的概率为![]() 。本题考查古典概型,注意任选是无顺序的。
。本题考查古典概型,注意任选是无顺序的。
试题解析:设3名男生编号为A1,A2,A3,两名女生的编号为B1,B2,那么从5人中任选两人,可能的结果为:(A1,A2),(A1,A3),(A1,B1),(A1,B2),(A2,A3),(A2,B1),(A2,B2),(A3,B1),(A3,B2),(B1,B2),共10种。
(1)设“所选2人都是男生”的事件为![]() ,
,
则![]() 包含3个基本事件,所以:
包含3个基本事件,所以:![]() ;
;
(2)设“所选2人恰有1名女生”的事件为![]() ,
,
则![]() 包含6个基本事件,所以:
包含6个基本事件,所以:![]() ;
;
(3)设“所选2人至少有1名女生”的事件为![]() ,分两种情况:①2名都是女生,基本事件有1个;②恰有1名女生,基本事件有6个,
,分两种情况:①2名都是女生,基本事件有1个;②恰有1名女生,基本事件有6个,
所以:![]()


 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案科目:高中数学 来源: 题型:
【题目】如(1)图所示,在直角梯形ABCD中,AD∥BC,![]() ,AB=BC=1,AD=2,E是AD的中点,O是AC与BE的交点.将△ABE沿BE折起到△A1BE的位置,如图(2)所示.
,AB=BC=1,AD=2,E是AD的中点,O是AC与BE的交点.将△ABE沿BE折起到△A1BE的位置,如图(2)所示.
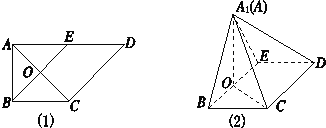
(1)证明:CD⊥平面A1OC;
(2)若平面A1BE⊥平面BCDE,求平面A1BC与平面A1CD所成锐二面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】关于直线的倾斜角与斜率,下列说法正确的是( )
A.所有的直线都有倾斜角和斜率
B.所有的直线都有倾斜角但不一定都有斜率
C.直线的倾斜角和斜率有时都不存在
D.所有的直线都有斜率,但不一定有倾斜角
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,![]() 为圆
为圆![]() 上的动点,定点
上的动点,定点![]() ,线段
,线段![]() 的垂直平分线交线段
的垂直平分线交线段![]() 于点
于点![]() .
.
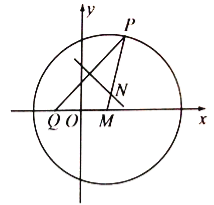
(1)求动点![]() 的轨迹方程;
的轨迹方程;
(2)记动点![]() 的轨迹为曲线
的轨迹为曲线 ![]() ,设圆
,设圆![]() 的切线
的切线![]() 交曲线
交曲线![]() 于
于![]() 两点,求
两点,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知矩形![]() 所在平面垂直于直角梯形
所在平面垂直于直角梯形![]() 所在平面,平面
所在平面,平面![]() 平面
平面![]() ,且
,且![]() ,且
,且![]() .
.

(1)设点![]() 为棱
为棱![]() 中点,在面
中点,在面![]() 内是否存在点
内是否存在点![]() ,使得
,使得![]() 平面
平面![]() ?若存在,请证明,若不存在,说明理由;
?若存在,请证明,若不存在,说明理由;
(2)求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com