
【题目】在底面是菱形的四棱锥![]() 中,
中,![]() .
.
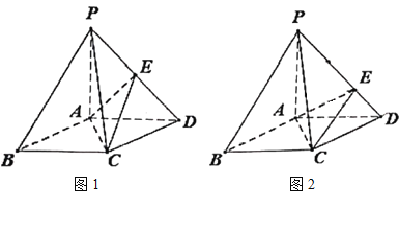
(1)证明:![]() 平面
平面![]() ;
;
(2)点![]() 在棱
在棱![]() 上.
上.
①如图1,若点![]() 是线段
是线段![]() 的中点,证明:
的中点,证明:![]() 平面
平面![]() ;
;
②如图2,若![]() ,在棱
,在棱![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() 平面
平面![]() ?证明你的结论.
?证明你的结论.
【答案】(1)证明见解析;(2)①证明见解析;②存在,证明见解析
【解析】
(1)首先根据题意得到![]() 是等边三角形,根据勾股定理得到
是等边三角形,根据勾股定理得到![]() ,
,![]() ,再根据线面垂直的判定即可证明
,再根据线面垂直的判定即可证明![]() 平面
平面![]() .
.
(2)①根据三角形中位线即可得到![]() ,再根据线面平行的判定即可证明
,再根据线面平行的判定即可证明![]() 平面
平面![]() .②存在
.②存在![]() 是
是![]() 中点,使得
中点,使得![]() 平面
平面![]() ,取
,取![]() 中点
中点![]() ,连结
,连结![]() .根据三角形中位线即可得到
.根据三角形中位线即可得到![]() 面
面![]() ,
,![]() 面
面![]() ,即平面
,即平面![]() 平面
平面![]() ,再利用面面平行的性质即可得到
,再利用面面平行的性质即可得到![]() 平面
平面![]() .
.
(1)在菱形![]() 中,
中,![]()
![]() ,
,
∴![]() 是等边三角形.
是等边三角形.
又![]() ,故菱形边长为
,故菱形边长为![]() ,
,
在![]() 中,
中,![]() ,则
,则![]()
同理![]() .
.
又![]() 面
面![]() ,
,![]() ,
,
∴![]() 平面
平面![]() .
.
(2)①连结![]() 交
交![]() 于
于![]() ,连接
,连接![]() .
.
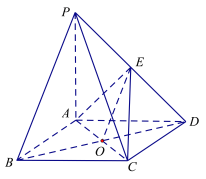
在菱形![]() 中
中![]() 为
为![]() 中点又
中点又![]() 是线段
是线段![]() 的中点,
的中点,
所以![]() .
.
∵![]() 面
面![]() ,
,![]() 面
面![]() ,
,
∴![]() 面
面![]() .
.
②存在,![]() 是
是![]() 中点.
中点.
取![]() 中点
中点![]() ,连结
,连结![]() .
.
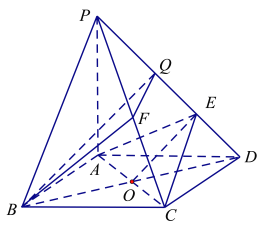
在![]() 中
中![]() ,
,![]() 为
为![]() 中点,则
中点,则![]() ,
,
又∵![]() 面
面![]() ,
,![]() 面
面![]() ,∴
,∴![]() 面
面![]() .
.
同理![]() 面
面![]() .
.
又∵![]() 面
面![]() ,
,![]() ,
,
所以平面![]() 平面
平面![]() ,
,
又![]() 面
面![]() ∴
∴![]() 平面
平面![]() .
.


科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为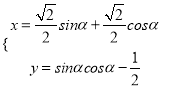 (
(![]() 为参数),若以直角坐标系中的原点为极点,
为参数),若以直角坐标系中的原点为极点, ![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() (
(![]() 为实数.)
为实数.)
(1)求曲线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)若曲线![]() 与曲线
与曲线![]() 有公共点,求
有公共点,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=sin(2x+![]() )+cos(2x﹣
)+cos(2x﹣![]() )+cos2x﹣sin2x,x∈R.
)+cos2x﹣sin2x,x∈R.
(1)求函数f(x)的最小正周期及单调递增区间;
(2)求函数f(x)在区间[﹣![]() ]上的最大值和最小值.
]上的最大值和最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】①回归分析中,相关指数![]() 的值越大,说明残差平方和越大;
的值越大,说明残差平方和越大;
②对于相关系数![]() ,
,![]() 越接近1,相关程度越大,
越接近1,相关程度越大,![]() 越接近0,相关程度越小;
越接近0,相关程度越小;
③有一组样本数据![]() 得到的回归直线方程为
得到的回归直线方程为![]() ,那么直线
,那么直线![]() 必经过点
必经过点![]() ;
;
④![]() 是用来判断两个分类变量是否有关系的随机变量,只对于两个分类变量适合;
是用来判断两个分类变量是否有关系的随机变量,只对于两个分类变量适合;
以上几种说法正确的序号是__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知平面四边形MNPQ中,MN=![]() ,MP=1,MP⊥MN,PQ⊥QM.
,MP=1,MP⊥MN,PQ⊥QM.
(Ⅰ)若PQ=![]() ,求NQ的值;
,求NQ的值;
(Ⅱ)若∠MQN=30°,求sin∠QMP的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在一次演唱会上共10 名演员(每名演员都会唱歌或跳舞),其中7人能唱歌,6人会跳舞.
(1)问既能唱歌又会跳舞的有几人?
(2)现要选出一个2人唱歌2人伴舞的节目,有多少种选派方法?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有甲乙两个班级进行数学考试,按照大于等于85分为优秀,85分以下为非优秀统计成绩后,得到如下的列联表.
| 优秀 | 非优秀 | 总计 |
甲班 | 10 | ||
乙班 | 30 | ||
总计 | 105 |
已知在全部105人中随机抽取1人为优秀的概率为![]() .
.
(1)请完成上面的列联表;(把列联表自己画到答题卡上)
(2)根据列联表的数据,若按95%的可靠性要求,能否认为“成绩与班级有关系”?
参考公式:![]()
P(K2≥k0) | 0.10 | 0.05 | 0.025 | 0.010 |
k0 | 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 的前
的前![]() 项和为
项和为![]() ,满足
,满足![]() ,
,![]() ,数列
,数列![]() 满足
满足![]() ,
,![]() ,且
,且![]() .
.
(1)求数列![]() 的通项公式;
的通项公式;
(2)求证:数列![]() 是等差数列,求数列
是等差数列,求数列![]() 的通项公式;
的通项公式;
(3)若![]() ,数列
,数列![]() 的前
的前![]() 项和为
项和为![]() ,对任意的
,对任意的![]() ,都有
,都有![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com