练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知抛物线C1：y= x2（p＞0）的焦点与双曲线C2： ﹣y2=1的右焦点的连线交C1于第一象限的点M，若C1在点M处的切线平行于C2的一条渐近线，则p=（ ）
    A.
    B.
    C.
    D.

    【答案】D
    【解析】解：由抛物线C1：y= x2（p＞0）得x2=2py（p＞0）， 所以抛物线的焦点坐标为F（0， ）．
    由 ﹣y2=1得a= ，b=1，c=2．
    所以双曲线的右焦点为（2，0）．
    则抛物线的焦点与双曲线的右焦点的连线所在直线方程为 ，
    即 ①．
    设该直线交抛物线于M（ ），则C1在点M处的切线的斜率为 ．
    由题意可知 = ，得x0= ，代入M点得M（ ， ）
    把M点代入①得： ．
    解得p= ．
    故选：D．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】函数f（x）=（x2﹣2x﹣3）的单调减区间是（　　）
    A.（3，+∞）
    B.（1，+∞）
    C.（﹣∞，1）
    D.（﹣∞，﹣1）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】为丰富中学生的课余生活，增进中学生之间的交往与学习，某市甲乙两所中学举办一次中学生围棋擂台赛．比赛规则如下，双方各出3名队员并预先排定好出场顺序，双方的第一号选手首先对垒，双方的胜者留下进行下一局比赛，负者被淘汰出局，由第二号选手挑战上一局获胜的选手，依此类推，直到一方的队员全部被淘汰，另一方算获胜．假若双方队员的实力旗鼓相当（即取胜对手的概率彼此相等） （Ⅰ）在已知乙队先胜一局的情况下，求甲队获胜的概率．
    （Ⅱ）记双方结束比赛的局数为ξ，求ξ的分布列并求其数学期望Eξ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）的定义域为D，若对于a，b，c∈D，f（a），f（b），f（c）分别为某个三角形的三边长，则称f（x）为“三角形函数”．给出下列四个函数： ①f（x）=lg（x+1）（x＞0）；
    ②f（x）=4﹣cosx；
    ③ ；
    ④
    其中为“三角形函数”的个数是（ ）
    A.1
    B.2
    C.3
    D.4

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知抛物线C的顶点在坐标原点，焦点F在x轴的正半轴上，过点F的直线l与抛物线C相交于A、B两点，且满足 ．
    （1）求抛物线C的标准方程；
    （2）若点M在抛物线C的准线上运动，其纵坐标的取值范围是[﹣1，1]，且 ，点N是以线段AB为直径的圆与抛物线C的准线的一个公共点，求点N的纵坐标的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）=ax+x2﹣xlna（a＞0，a≠1）．
    （Ⅰ）当a＞1时，求证：函数f（x）在（0，+∞）上单调递增；
    （Ⅱ）若函数y=|f（x）﹣t|﹣1有三个零点，求t的值；
    （Ⅲ）若存在x1 ， x2∈[﹣1，1]，使得|f（x1）﹣f（x2）|≥e﹣1，试求a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，四边形ABCD为正方形，PD⊥平面ABCD，PD∥QA，QA=AB= PD．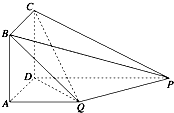

    （1）证明：平面PQC⊥平面DCQ；
    （2）求二面角Q﹣BP﹣C的正弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设函数f（x）=（x+b）lnx，g（x）=alnx+ ﹣x（a≠1），已知曲线y=f（x）在点（1，f（1））处的切线与直线x+2y=0垂直．
    （1）求b的值；
    （2）若对任意x≥1，都有g（x）＞ ，求a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】平面直角坐标系xOy中，椭圆C： =1（a＞b＞0）的长轴长为2，抛物线E：x2=2y的准线与椭圆C相切．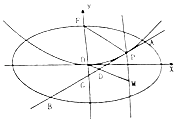

    （Ⅰ）求椭圆C的方程；
    （Ⅱ）若直线l与椭圆C相交于A，B两点且与抛物线E在第一象限相切于点P，线段AB的中点为D，直线OD与过P且垂直于x轴的直线交于点M，求 的最小值及此时点P的坐标．

    查看答案和解析>>

    同步练习册答案