分析:(1)将n分别用1,2 代替求出C
1,C
2,利用多项式的乘法展开,求出C
1,C
2的小数部分B
1,B
2,求出C
1B
1,C
2B
2的值.
(2)利用二项式定理表示出C
n,再利用二项式定理表示出
(+1)2n-1,两个式子相减得到展开式的整数部分和小数部分,求出C
nB
n的值,从而证得结论.
解答:解:(1)由于
Cn=(+1)2n-1,所以,C
1=
+1 B
1=
-1 A
1=2,所以C
1B
1=2.
又C
2=
(+1)3=10+6
,其整数部分A
2=20,小数部分B
2=6
-10,
所以C
2B
2=8.
(2)证明:由于
Cn=(+1)2n-1=
•
()2n-1+
•
()2n-2+
•
()2n-3,
+…+
①,
又
(-1)2n-1=
•
()2n-1-
•
()2n-2+
•
()2n-3-
()2n-4+…+
②,
①-②可得,
(+1)2n-1-
(-1)2n-1=2(
•
()2n-2+
()2n-4+…+
),
而0<
(-1)2n-1<1,∴A
n=
(+1)2n-1-
(-1)2n-1,B
n=
(-1)2n-1.
故 C
nB
n=
(+1)2n-1•
(-1)2n-1=2
2n-1.
点评:解决二项式的有关问题一般利用二项式定理;解决二项展开式的通项问题常利用的工具是二项展开式的通项公式,属于中档题.



 星级口算天天练系列答案
星级口算天天练系列答案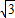 +1)2n-1(n∈N*)的整数部分为An,小数部分为Bn.
+1)2n-1(n∈N*)的整数部分为An,小数部分为Bn.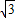 +1)2n-1(n∈N*)的整数部分为An,小数部分为Bn.
+1)2n-1(n∈N*)的整数部分为An,小数部分为Bn.