
【题目】已知![]() .
.
(1)将![]() 的单调区间和极值;
的单调区间和极值;
(2)若![]() 有两个零点
有两个零点![]() ,求
,求![]() 的取值范围,并证明
的取值范围,并证明![]() .
.
【答案】(1)![]() 在区间
在区间![]() 上单调递减,在区间
上单调递减,在区间![]() 上单调递增;
上单调递增;![]() 有极小值
有极小值![]() ,无极大值;(2)
,无极大值;(2)![]() ,证明见解析.
,证明见解析.
【解析】
(1)求得函数的导数![]() ,求得函数的单调性,根据函数极值的概念,即可求解;
,求得函数的单调性,根据函数极值的概念,即可求解;
(2)由(1)和题设条件得到极小值![]() ,令
,令![]() ,化简得到函数
,化简得到函数![]() ,进而求得
,进而求得![]() ,再由题目条件化简得
,再由题目条件化简得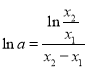 ,
,
利用分析法,即可证得结论.
(1)由题意,函数![]() ,则
,则![]() ,
,
令![]() ,即
,即![]() ,可得
,可得![]() ,解得
,解得![]() ,
,
令![]() ,即
,即![]() ,可得
,可得![]() ,解得
,解得![]() ,
,
所以函数![]() 在区间
在区间![]() 上单调递减,在区间
上单调递减,在区间![]() 上单调递增,
上单调递增,
所以当![]() 时,函数
时,函数![]() 取得极小值,
取得极小值,
极小值为![]() ,无极大值.
,无极大值.
(2)由(1)可知,若函数![]() 有两零点,则极小值
有两零点,则极小值![]() ,
,
所以![]() ,可得
,可得![]() ,即
,即![]() ,且极值点
,且极值点![]() ,
,
又由![]() ,
,
令![]() ,则
,则![]() ,
,![]() ,
,
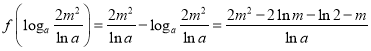 ,
,
令![]() ,
,![]() ,
,
![]() 在
在![]() 上单调递增,所以
上单调递增,所以![]()
所以![]() ,所以
,所以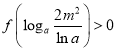 ,
,
从而可得![]() 在
在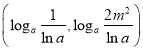 上有一个零点,
上有一个零点,
所以当![]() 时,
时,![]() 在区间
在区间![]() 各有唯一零点
各有唯一零点
由题目条件可得![]() ,两边同时取对数可得
,两边同时取对数可得![]() ,
,![]() ,
,
两式相减可得![]() ,即
,即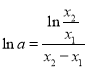 ,
,
要证![]() ,
,
只需证![]() ,即证
,即证 ,即证
,即证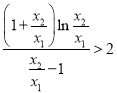 ,
,
即证  即证
即证 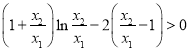 ,
,
令 ![]() ,则
,则![]() ,只需要证
,只需要证![]() ,
,
令![]() ,则
,则![]() ,可得
,可得![]() ,
,
当![]() 时
时![]() ,所以
,所以![]() 在
在![]() 上单调递增,
上单调递增,
所以当![]() 时
时![]() ,所以
,所以![]() 在
在 ![]() 上单调递增,
上单调递增,
当![]() 时
时![]() ,即
,即![]() 在
在![]() 上恒成立.
上恒成立.
原命题得证.


 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案科目:高中数学 来源: 题型:
【题目】如图,CM,CN为某公园景观湖胖的两条木栈道,∠MCN=120°,现拟在两条木栈道的A,B处设置观景台,记BC=a,AC=b,AB=c(单位:百米)
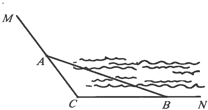
(1)若a,b,c成等差数列,且公差为4,求b的值;
(2)已知AB=12,记∠ABC=θ,试用θ表示观景路线A-C-B的长,并求观景路线A-C-B长的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】![]() 年上半年,随着新冠肺炎疫情在全球蔓延,全球超过
年上半年,随着新冠肺炎疫情在全球蔓延,全球超过![]() 个国家或地区宣布进人紧急状态,部分国家或地区直接宣布“封国”或“封城”,随着国外部分活动进入停摆,全球经济缺乏活力,一些企业开始倒闭,下表为
个国家或地区宣布进人紧急状态,部分国家或地区直接宣布“封国”或“封城”,随着国外部分活动进入停摆,全球经济缺乏活力,一些企业开始倒闭,下表为![]() 年第一季度企业成立年限与倒闭分布情况统计表:
年第一季度企业成立年限与倒闭分布情况统计表:
企业成立年份 | 2019 | 2018 | 2017 | 2016 | 2015 |
企业成立年限 | 1 | 2 | 3 | 4 | 5 |
倒闭企业数量(万家) | 5.23 | 4.70 | 3.72 | 3.12 | 2.42 |
倒闭企业所占比例 | 21.8% | 19.6% | 15.5% | 13.0% | 10.1% |
根据上表,给出两种回归模型:
模型①:建立曲线型回归模型![]() ,求得回归方程为
,求得回归方程为![]() ;
;
模型②:建立线性回归模型![]() .
.
(1)根据所给的统计量,求模型②中![]() 关于
关于![]() 的回归方程;
的回归方程;
(2)根据下列表格中的数据,比较两种模型的相关指数![]() ,并选择拟合精度更高、更可靠的模型,预测
,并选择拟合精度更高、更可靠的模型,预测![]() 年成立的企业中倒闭企业所占比例(结果保留整数).
年成立的企业中倒闭企业所占比例(结果保留整数).
回归模型 | 模型① | 模型② |
回归方程 |
|
|
|
|
参考公式: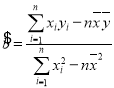 ,
,![]() ;
;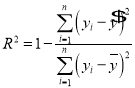 .
.
参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,斜率为![]() 的直线交抛物线
的直线交抛物线![]() 于
于![]() 两点,已知点
两点,已知点![]() 的横坐标比点
的横坐标比点![]() 的横坐标大4,直线
的横坐标大4,直线![]() 交线段
交线段![]() 于点
于点![]() ,交抛物线于点
,交抛物线于点![]() .
.
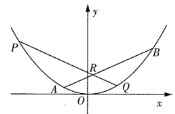
(1)若点![]() 的横坐标等于0,求
的横坐标等于0,求![]() 的值;
的值;
(2)求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知正三棱柱ABC﹣A1B1C1的底面边长为![]() ,且该三棱柱外接球的表面积为14π,若P为底面A1B1C1的中心,则PA与平面ABC所成角的大小为( )
,且该三棱柱外接球的表面积为14π,若P为底面A1B1C1的中心,则PA与平面ABC所成角的大小为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)![]() |2x﹣3|,g(x)
|2x﹣3|,g(x)![]() |2x+a+b|.
|2x+a+b|.
(1)解不等式f(x)![]() x2;
x2;
(2)当a![]() 0,b
0,b![]() 0时,若F(x)
0时,若F(x)![]() f(x)+g(x)的值域为[5,+∞),求证:
f(x)+g(x)的值域为[5,+∞),求证:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现有一种水上闯关游戏,共设有3个关口,如果在规定的时间内闯过了这3个关口,那么闯关成功,否则闯关失败,结束游戏.假定小张、小王、小李闯过任何一个关口的概率分别为![]() ,且各关口能否顺利闯过相互独立.
,且各关口能否顺利闯过相互独立.
(1)求小张、小王、小李分别闯关成功的概率;
(2)记小张、小王、小李三人中闯关成功的人数为X,求X的分布列及数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com